Contents
In this publication, we will consider the definition of a segment of a circle and the formulas with which you can calculate its area (in terms of the radius and central angle of the circular sector). We will also analyze examples of solving problems to demonstrate the practical application of formulas.
Circle Segment Definition
circle segment – this is the part that is bounded by an arc of a circle and its chord.
Chord – this is the part of the straight line (secant) that intersects the circle. The ends of the chord are connected to the center of the circle, resulting in an isosceles triangle, the sides of which are the radius of the circle. If you add a segment to this triangle, you get a sector.
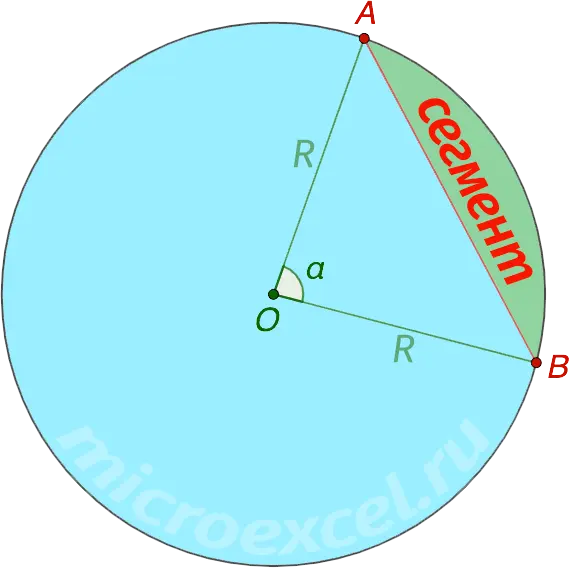
In the picture above:
- the segment of the circle is shaded green;
- line segment AB – this is a chord;
- part of a circle between points AB – arc of a circle;
- R is the radius of the circle;
- α is the angle of the sector.
Formulas for finding the area of a circular segment
Through radius and central angle in degrees
![]()
a° is the angle in degrees.
Note: value is used in calculations π, approximately equal to the number 3,14.
Through the radius and angle of the sector in radians
![]()
αglad is the angle in radians.
Task examples
Task 1
Find the area of a segment of a circle if its radius is 8 cm and the central angle of the sector that subtends the segment is 45 degrees.
Solution
Let’s use the first formula, substituting the known values into it:
![]()
Task 2
The area of the circular segment is 24 cm2, and the central angle of the sector of the circle, of which the segment is a part, is equal to 1 radian. Find the radius of the circle.
Solution
In this case, we can get the radius from a formula that uses an angle in radians:










