Contents
In this publication, we will consider formulas that can be used to calculate the area of a sector of a circle, as well as analyze examples of solving problems to demonstrate their practical application.
Definition of a sector of a circle
Circle sector is the part formed by its two radii and the arc between them. In the figure below, the sector is shaded in green.
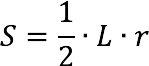
- AB – sector arc;
- R (or r) is the radius of the circle;
- α is the angle of the sector, i.e. angle between two radii. It is also sometimes called the central angle.
Formulas for finding the area of a sector of a circle
Through the length of the arc and the radius of the circle
Area (S) of a sector of a circle is equal to one second of the product of the arc length of the sector (L) and radius of the circle (r).
![]()
Through the angle of the sector (in degrees) and the radius of the circle
Area (S) of a sector of a circle equals the area of the circle multiplied by the angle of the sector in degrees (a°) and divided by 360°.
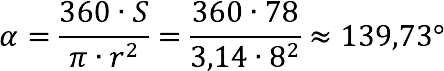
Through the angle of the sector (in radians) and the radius of the circle
Area (S) of a sector of a circle is equal to half the product of the angle of the sector in radians (aglad) and the square of the radius of the circle.
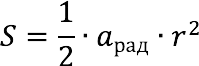
Examples of tasks
Task 1
A circle with a radius of 6 cm is given. Find the area of a sector if it is known that the length of its arc is 15 cm.
Solution
Let’s use the first formula, substituting the given values into it:
![]()
Task 2
Find the angle of a sector if its area is known to be 78 cm2, and the radius of the circle is 8 cm.
Solution
We derive a formula for finding the central angle from the second formula discussed above:
![]()









