Contents
In this publication, we will consider how to calculate the surface area of a regular prism of various types (triangular, quadrangular and hexagonal), and also, we will analyze examples of solving problems for fixing the material.
Correct prism is a straight prism whose base is a regular polygon. A straight figure is in the event that its side faces are perpendicular to the bases.
The formula for the area of a regular prism
1. General formula
The area (S) of the total surface of the prism is equal to the sum of the area of its side surface and the two areas of the base.
Sfull = Sside. + 2Smain
The area of the lateral surface of a straight prism is equal to the product of the perimeter of its base and the height.
Sside. = Pmain ⋅ h
The formula for the perimeter and area of uXNUMXbuXNUMXbthe base of a regular prism depends on the type of polyhedron. Below we will look at the most popular types.
2. Area of a regular triangular prism
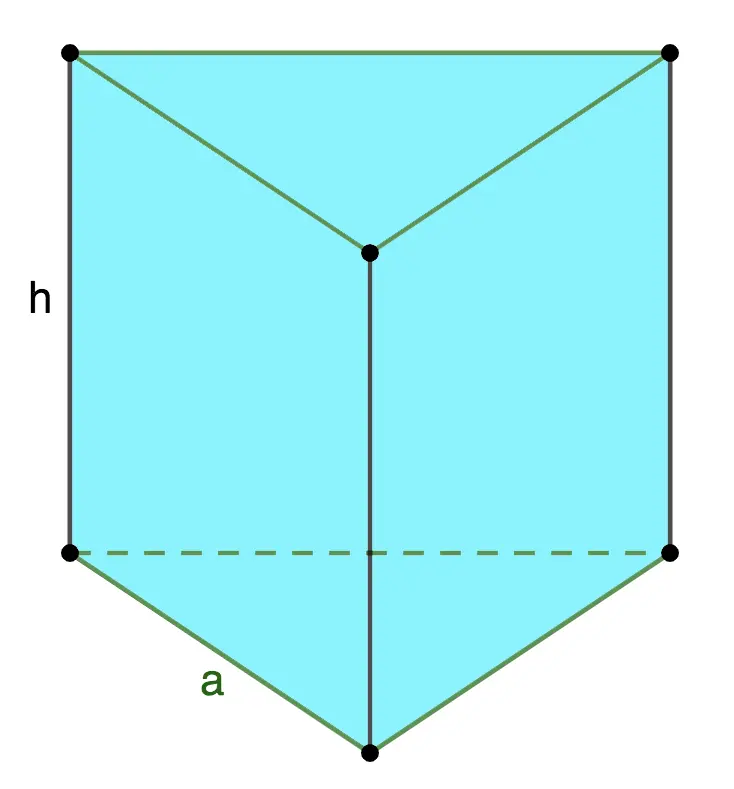
Base: equilateral triangle.
» data-order=» «>
«>
» data-order=» «>
«>
| Area | Formula |
| base | |
| side surface | full |
3. Area of a regular quadrangular prism
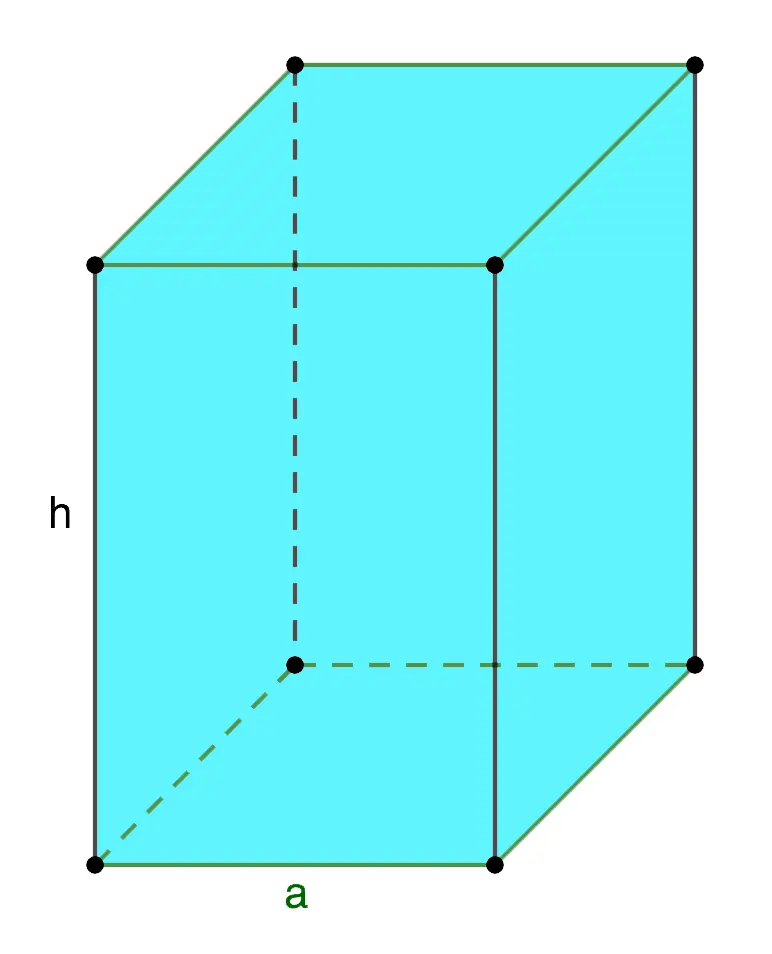
Base: square.
| Area | Formula | |||||||
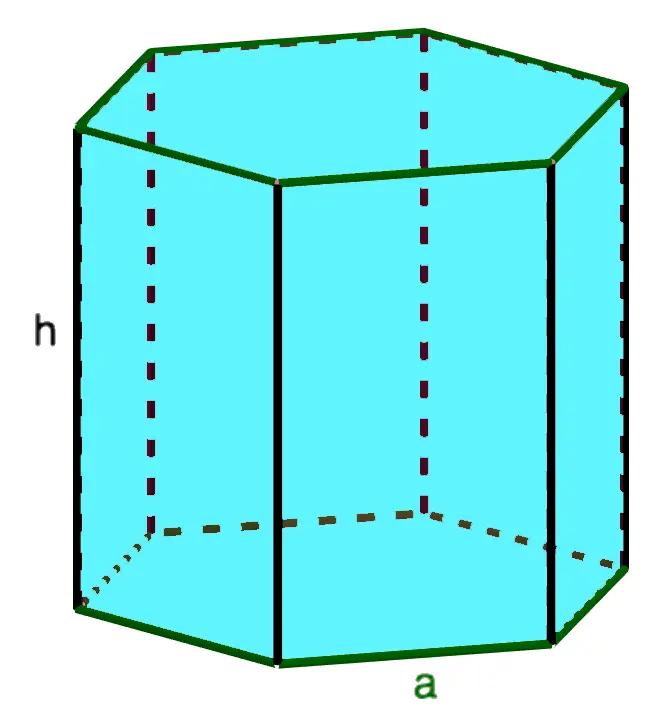
| base | side surface | full | 4. Площадь правильной шестиугольной призмы
Base: regular hexagon » data-order=» » data-order=»
microexcel.ru Examples of tasksExercise 1: The side of a regular triangular prism is 6 cm and its height is 8 cm. Find the total surface area of the figure. Decision: Let’s use the appropriate formula, substituting the known values into it:
Exercise 2: The total surface area of a regular hexagonal prism is 400 cm2. Find its height if it is known that the side of the base is 5 cm. Decision: We derive an expression for finding the height of the prism from the formula for its total area:
Leave a commentОтменить ответ |










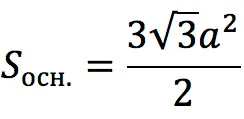 «>
«>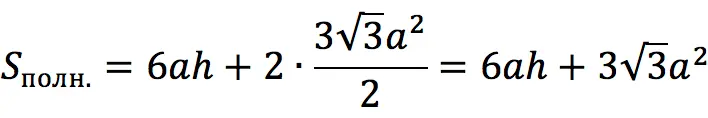 «>
«>