Contents
In this publication, we will consider formulas that can be used to calculate the length of the arc of a sector of a circle, as well as analyze examples of solving problems to demonstrate their application in practice.
Determining the Arc of a Sector of a Circle
Arc is the area between two points on the circle.
Long sector of a circle – this is the area between two points on a circle, which are obtained as a result of the intersection of this circle with two radii that form a sector of the circle.
In the picture below: AB is the arc of the green sector of the circle with radius R (or r).
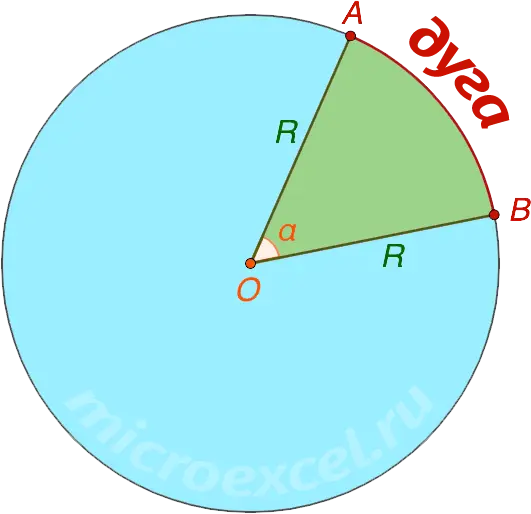
- OA = OB = R (r);
- α – sector angle or central angle.
Formulas for finding the arc length of a sector
Through the central angle in degrees and the radius
Length (L) sector arc equals the number π, multiplied by the radius of the circle (r) times the central angle in degrees (a°), divided by 180°.
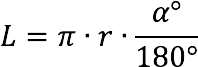
Note: number is used in calculations π, approximately equal to 3,14.
Through the sector angle in radians and the radius
Length (L) of the arc of the sector is equal to the product of the radius (r) and central angle expressed in radians (aglad).
![]()
Examples of tasks
Task 1
Given a circle with a radius of 15 cm. Find the length of the arc of a sector whose angle is 30°.
Solution
Let’s use the calculation formula, which uses the central angle in degrees:
![]()
Task 2
The arc length of the sector is 24 cm. Find its angle (in radians and degrees) if the radius of the circle is 12 cm.
Solution
First, let’s calculate the angle in radians:
![]()
1 radian ≈ 57,2958°
Therefore, the central angle is approximately 114,59° (2 rad ⋅ 57,2958°).









