Finding the angle between vectors

In this publication, we will consider what an angle between two vectors is, and give a formula with which you can find its cosine. We will also analyze an example of solving a problem on this topic.

Finding the angle between vectors

Angle between two vectorsoriginating at the same point is the smallest angle that one of the given vectors can rotate around its starting point to a position at which it will be co-directed with the second vector.

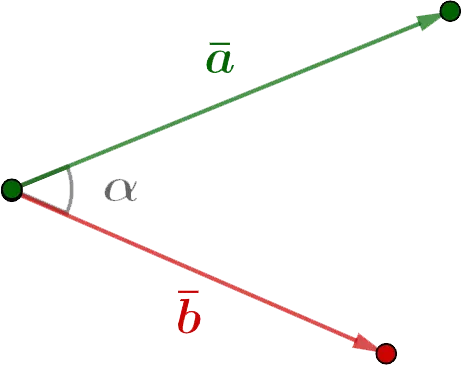
Cosine of the angle between two vectors equals the scalar product of vectors divided by the product of the lengths (modules) of these vectors.

The formula below is used to calculate the cosine of an angle:

Example of a problem

Find the angle between vectors a = {4; 3} и b = {12; 5}.

Solution

1. First, let’s calculate their scalar product:

a · b = 4 · 12 + 3 · 5 = 48 + 15 = 63.

2. Now let’s find the lengths (modules) of the given vectors:

3. Apply the formula for finding the cosine of an angle:

4. Therefore, the angle is approximately 14,26° (arccos 0,9692).