Fibonacci numbers is a sequence of numbers that begins with the digits 0 and 1, and each subsequent value is the sum of the two previous ones.
Content
Fibonacci Sequence Formula
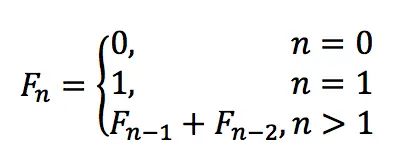
For example:
- F0 = 0
- F1 = 1
- F2 = F1+F0 = 1+0 = 1
- F3 = F2+F1 = 1+1 = 2
- F4 = F3+F2 = 2+1 = 3
- F5 = F4+F3 = 3+2 = 5
Golden Section
The ratio of two consecutive Fibonacci numbers converges to the golden ratio:
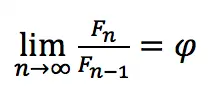
where φ is the golden ratio = (1 + √5) / 2 ≈ 1,61803399
Most often, this value is rounded up to 1,618 (or 1,62). And in rounded percentages, the proportion looks like this: 62% and 38%.
Fibonacci Sequence Table
| n | 0 | 0 |
| 1 | 1 | |
| 2 | 1 | |
| 3 | 2 | |
| 4 | 3 | |
| 5 | 5 | |
| 6 | 8 | |
| 7 | 13 | |
| 8 | 21 | |
| 9 | 34 | |
| 10 | 55 | |
| 11 | 89 | |
| 12 | 144 | |
| 13 | 233 | |
| 14 | 377 | |
| 15 | 610 | |
| 16 | 987 | |
| 17 | 1597 | |
| 18 | 2584 | |
| 19 | 4181 | |
| 20 | 6765 |
microexcel.ru
C-code (C-code) functions
double Fibonacci(unsigned int n) { double f_n =n; double f_n1=0.0; double f_n2=1.0; if( n > 1 ) { for(int k=2; k









