Exponent: definition, formula, properties, graph

In this publication, we will consider what an exponent is, what its graph looks like, give a formula that defines an exponential function, and also list its main properties.

Exponent definition and formula

Exhibitor is an exponential function, the formula of which is as follows:

f (x) = exp(x) = e ^x

where e -.

An exponential function (as the exponent is often called) can be defined:

Through the limit (lim):

Through the Taylor power series:

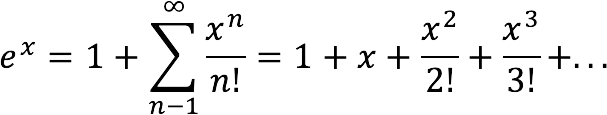
Exhibitor chart

Below is a graph of the exponential function y=e ^x.

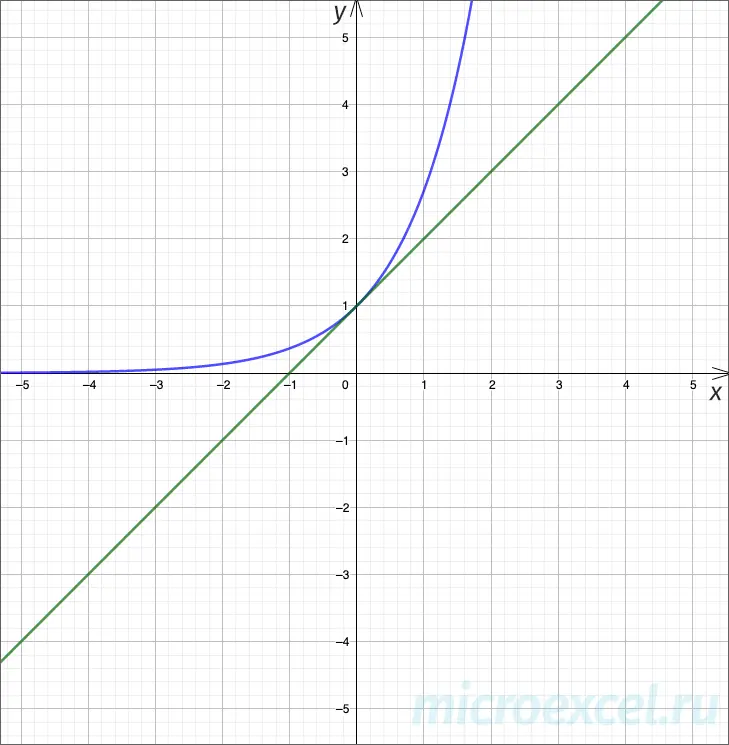
As we can see, the graph (blue line) is convex, strictly increasing, i.e. with increasing x value increases y.

Asymptote is the x-axis, i.e. graph in the second quarter of the coordinate plane tends to the axis Ox, but will never cross or touch it.

Intersection with the y-axis Oy – at the point (0, 1)As e⁰ = 1.

Tangent (green line) to the exponent passes at an angle of 45 degrees at the point of contact.

Properties of the exponential function

1. Exponent defined for all x, and the function is increasing everywhere, and its value is always greater than zero. That is:
   • domain: – ∞ x + ∞;
   • range: 0 y < + ∞.
2. The function inverse to the exponent is (ln x).
   • ln e ^x = x;
   • e ^{ln x} = xWhere x > 0.
3. For the exponent, for example: e ^(a+b) = and ^a ⋅ and ^b.
4. Derivative of the exponent:
   • (e ^x)‘ = and ^x.
   • if instead of x – complex function u: (e ^u)‘ = and ^u +u‘.
5. Exponential Integral: ∫e ^x dx = e ^x + CWhere C is the integration constant.