Euler number (e)

Number e (or, as it is also called, the Euler number) is the base of the natural logarithm; a mathematical constant that is an irrational number.

e = 2.718281828459 …

Ways to determine the number e (formula):

1. Through the limit:

Second remarkable limit:

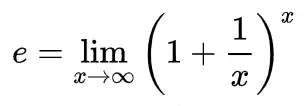
Alternative option (follows from the De Moivre-Stirling formula):

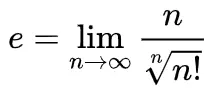
2. As a series sum:

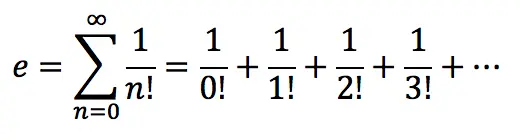
number properties e

1. Reciprocal limit e

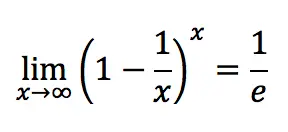
2. Derivatives

The derivative of the exponential function is the exponential function:

(e ^x)′ = and^x

The derivative of the natural logarithmic function is the inverse function:

(log_e x)′ = (ln x)′ = 1/x

3. Integrals

The indefinite integral of an exponential function e ^x is an exponential function e ^x.

∫ and^x dx = e^x+c

The indefinite integral of the natural logarithmic function log_e x:

∫ log_e x dx = ∫ lnx dx = x ln x – x + c

Definite integral of 1 to e inverse function 1/x is equal to 1:

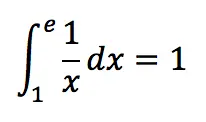
Logarithms with base e

Natural logarithm of a number x defined as the base logarithm x with base e:

ln x = log_e x

Exponential Function

This is an exponential function, which is defined as follows:

f (x) = exp(x) = e^x

Euler formula

Complex number e ^iθ equals:

e^iθ = cos (θ) + i sin (θ)

where i is the imaginary unit (the square root of -1), and θ is any real number.