Contents
Greetings to regular readers and visitors of the site! Eudoxus of Cnidus is an ancient Greek mathematician, mechanic, astronomer, geographer, physician, philosopher, musician, orator and lawyer. I hope that this article about the brilliant scientist will be of interest to you.
Biography of Eudoxus of Knidsky
A long time ago, yet our era, one of the most prominent scientists of Ancient Greece was born in the city of Cnidus.
Eudoxus was 23 years old when he came to Athens to listen to lectures at the Academy of the great Plato. The famous saying was engraved above the entrance to the Academy: “Let not one who is not trained in mathematics enter here”.
Here he solved a complex astronomical problem proposed by Plato. He created a model in which the movement of the Sun, Moon and planets was presented as a union of equal circular motions of the spheres. In the center was the Earth. The Eudoxus model marked the beginning of a new era in the history of astronomy.
Then there was a trip to Egypt. Eudoxus communicated with local priests in order to penetrate the laws of the movement of heavenly bodies, the secrets of the universe, and numerical relationships that they received.
Returning, the scientist founded a school of mathematicians and astronomers in the city of Kizika, on the shores of the Sea of Marmara. There he equipped one of the best astronomical observatories for its time. Astronomical observations were carried out here, thanks to which the country’s first star catalog was compiled.
In 365 BC. for the second time, now with his students, he visited Athens. He had long conversations with Plato on various scientific, primarily philosophical topics.
The authority and fame of the scientist attracted numerous students to him. He passed on the acquired knowledge to them, developed new scientific problems together with them, educating new researchers. Eudoxus of Cnidus died at the age of 53 in his native Cnidus, receiving well-deserved fame and honors. He had three daughters and a son.
Contribution to science by Eudoxus of Cnidus
None of Eudoxus’ works have survived to this day. Therefore, historians of science had to carry out colossal work in order to identify his contribution to science from the books of other authors, incidental references.
At first glance, it may seem that a mathematician discovers and shows his theorems independently of the events of the surrounding world. The biographies of most mathematicians, including Eudoxus, convince us that this is not the case.
To understand the incentives for Eudoxus’ mathematical quest, it is sufficient to at least briefly familiarize oneself with the situation in Greek mathematics at that time.
The discovery of incommensurability dealt a crushing blow to the Pythagorean philosophy of the omnipotence of a positive rational number.
Mathematicians were still living under the yoke of this surprise when the philosopher Zeno of Elea formulated his 45 aporias. In them, he showed the inconsistency of the concepts of motion, space and time, infinity and continuity, as well as the difficulty of expressing movement in the logic of concepts.
The discovery of incommensurable segments and the aporia of Zeno of Elea caused the first crisis in the methodological foundations of mathematics. They showed that some important mathematical concepts require deeper study and refinement, and the theoretical foundations of all mathematics require restructuring and strengthening.
The solution of these problems, which currently belong to mathematical analysis, was dedicated to his mathematical genius Eudoxus of Cnidus. He created new theoretical foundations of mathematics. First of all, the general doctrine of the relation, which basically coincides with the theory of real numbers.
A system close to it was built only in 1872 by the German mathematician Dedekind (1831 -1916). He discovered rigorous methods of passage to the limit. With their help, it was possible to solve many problems for calculating areas. This was the famous “exhausting method.”
Eudoxus was also the author of the method of proof. In the XVII century. it was called “apodictic”, or “method of reduction to absurdity.”
Clever Greeks!
Greek mathematicians have developed two ways to overcome the crisis in the theoretical foundations of their science.
Democritus of Abder (c. 460-370 BC) proposed to consider points as indivisible atoms. Moreover, in each segment they are always finite, although an extremely large number, when the plane is formed from straight lines, like a fabric woven from threads.
Democritus considered geometric bodies to be formed from parallel plates, the thickness of each of which is equal to an atom. In Democritus atomistic mathematics, all segments are commensurable, but new contradictions arise in it.
The second was the path of the so-called geometric algebra. Graphical (usually approximate) methods were developed for calculating the positive roots of equations of the first degree and square ones.
However, the methods of geometric algebra turned out to be powerless over equations of higher degrees. The results were approximate and were always presented in the form of some kind of geometric shapes.
The Greeks were the first to use fractions of the m / n type, although in the XNUMXth century. BC NS. there was not yet a sufficiently grounded theory, the introduction into science of these new mathematical objects and theories of operations with them. The mathematics already demanded more.
What was needed was a theory that introduced operations applicable to both rational and irrational numbers. Only with the help of a set of real numbers can the theory of measuring various quantities be substantiated. It is already surprising that the Greek scientists understood the need for such a theory.
And Eudoxus of Cnidus built it with such deep and logical perfection that only mathematicians of the late XNUMXth century understood all the greatness of his creation. The theory of the real number was developed. It turned out that it differs only in terminology and in some details from the theory of relations of Eudoxus of Cnidus.
Exhaustion method
With the help of the “method of exhaustion” Eudoxus proved a number of well-known, but not yet substantiated theorems. It was used by Euclid and Archimedes to calculate the areas, volumes and centers of gravity of geometric figures.
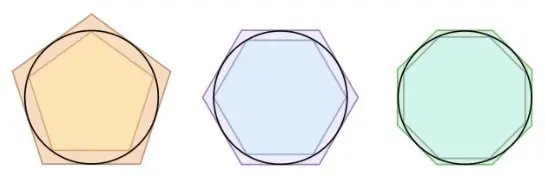
Calculating the area of a circle using other shapes – the “exhaustion method”
Now such problems are solved using integral calculus. Eudoxus’ method was more a method of proving known facts than discovering new ones. At the same time, this was the first doctrine of boundaries. Using this method, it was possible to compute the bounds of a wide class of sequences.
Eudoxus’ theories strengthened the theoretical foundations of mathematics and put an end to the first confusion. This gave scientists confidence in the reliability of mathematical theories.
Friends, if the article “Eudoxus of Cnidus: about the life of an ancient Greek mathematician” was useful for you, share it with your friends on social networks.









