Contents
In this publication, we will consider what elementary (equivalent) matrix transformations are, what types there are, and also analyze examples to demonstrate the theory in practice.
Definition and types of elementary transformations
Elementary Matrix transformations are called such transformations that preserve the equivalence of matrices (because of this they are often called equivalent). In other words, such transformations do not change the solution set , which is represented by the given matrix.
Elementary transformations are applied in the Gaussian method to bring the matrix to a triangular or stepped form.
The elementary transformations are:
- swapping any two strings;
- multiplying any string by a non-zero constant;
- the sum of any two strings, one of which is multiplied by a certain non-zero number.
Note: similar actions are applicable to the columns of the matrix.
Matrices A и B are equivalent, if B obtained by elementary transformations A (or vice versa). A special symbol is used to indicate equivalence – “~“Ie A ~ B.
Examples of equivalent matrix transformations
Let’s use the example of the matrix below to show all types of elementary transformations.

1. Swap the second and third lines in places.
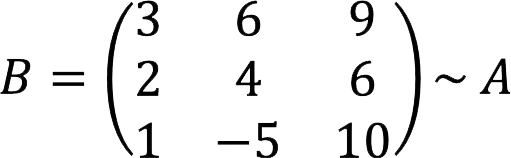
2. Multiply the first line by the number 3.
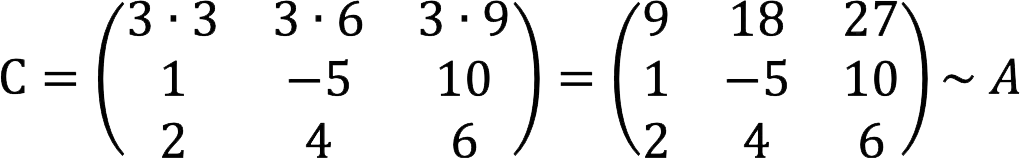
3. Subtract from the third row twice the second.










