In this publication, we will consider the rules and practical examples of how natural numbers (two-digit, three-digit and multi-digit) can be divided by a column – with and without a remainder.
Rules for dividing into a column
No leftovers
To find the quotient of dividing one number by another (with any number of digits), you can perform this arithmetic operation in a column.
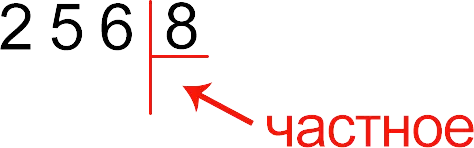
Consider the rules of division on a practical example for a better understanding. Let’s say we need to divide a three-digit number by a one-digit number, for example, 256 by 8. Here’s what we do:
1. We write the dividend (256), then we retreat a little from it and add the divisor (8) in the same line. Then between these numbers we draw a corner. The result will be written under the divisor.
2. In the dividend, from left to right, we count the minimum required number of digits so that the new number obtained from the digits contained in them is greater than the divisor. In our case, the number 2 is not enough, so we add 5 to it and as a result we get 25.

Note: If the leftmost digit of the dividend is greater than the divisor, there is no need to add the next digit to it, and we immediately proceed to the next step.
3. Determine how many integer times our divisor is contained in the divisible number obtained from the digits (25). In our case, three times. We write the number 3 in the space provided for this, then multiply it by the divisor
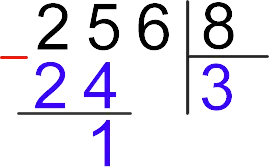
Note: Rules and examples for subtracting numbers in a column are given in a separate.
4. To the remainder (1) we add the next digit of the dividend (6) to get a new number, which is again greater than the divisor.
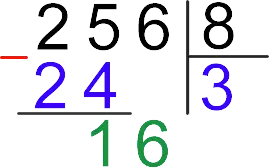
Note: If, when adding the next digit, the resulting new number is still less than the divisor, we take one more digit to the right (if possible), while writing zero in the quotient. Otherwise, division with a remainder is obtained, which we will consider next.
5. The number 16 contains exactly two times eight

On this division of the number 256 by 8 by a column was successfully completed, and the quotient is 32.
With the remainder
In general, the algorithm of actions is similar to the one described above. The only difference is that during the last subtraction, the remainder remains indivisible, to which there is nothing more to add from the divisible, because all of its ranks have already been used. The remainder is usually written to the right of the result in parentheses.
For example, the remainder of dividing 112 by 5 is two. That is
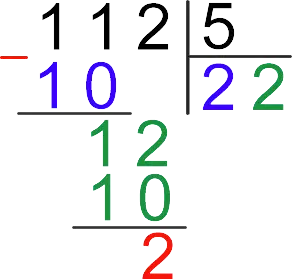
Explanation: subtracting 10 from 12 results in 2, but there is nothing more to add to it from the dividend.
Long division examples
Example 1
Divide a three-digit number by a two-digit number, for example 378 by 21.

Answer: 378: 21 = 18.
Example 2
Let’s find the quotient of dividing the numbers 1537 and 35.
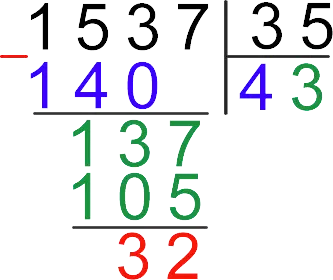
Explanation: in this case, in the dividend, you must immediately count from the left not two, but three digits, because the numbers 1 and 15 are less than 35.
Answer: 1537: 35 = 43 (32)









