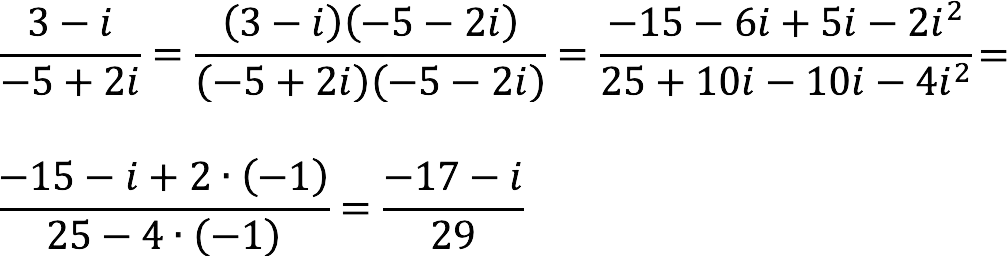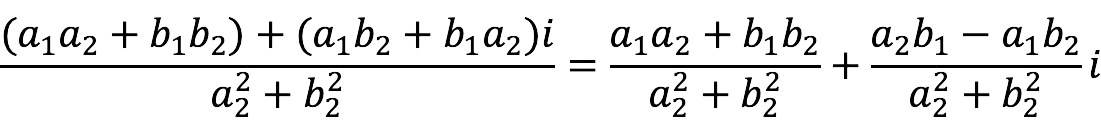Division of complex numbers

In this publication, we will consider formulas with which you can find the quotient of two complex numbers presented in algebraic or trigonometric form. Examples are also given for a better understanding of the theoretical material.

Division in algebraic form

The result of division (i.e. quotient) of two complex numbers x = a₁ + b₁i и y = to₂ + b₂i is also a complex number z:

The procedure is as follows:

1. We multiply the dividend and the divisor by the complex conjugate of the divisor. Let’s not forget that i² =-1.

   

   Note: For (a + bi) the complex conjugate will be the number (a – bi), i.e. the real part remains the same, but the imaginary part changes to the opposite.

2. As a result of performing multiplication in the denominator, an ordinary real number is obtained.

   (a₂ + b₂i)(a₂ – b₂i) = a₂ ⋅ a₂ – and₂ ⋅ b₂i + b₂i ⋅ a₂ – b₂i ⋅ b₂i = a₂² – b₂² ⋅ i² = a₂² + b₂².

3. Now let’s perform a similar action in the numerator:

   (a₁ + b₁i)(a₂ – b₂i) = a₁ ⋅ a₂ – and₁ ⋅ b₂i + b₁i ⋅ a₂ – b₁i ⋅ b₂i = a₁a₂ – b₁b₂i² – and₁b₂i + b₁a₂i = (a₁a₂ + b₁b₂) + (a₂b₁ – and₁b₂) ⋅ i.

4. Divide the resulting numerator by the denominator:

   

Example 1:

Divide a complex number (3 – i) on (-5 + 2i).

Decision:

We are guided by the action plan described above, and we get:

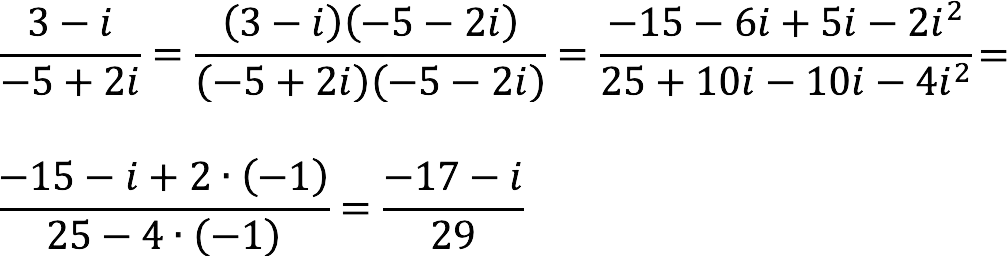
Division in geometric form

If complex numbers are given in trigonometric form, for example, x = |x| ⋅ (cos φ₁ + i ⋅ without φ₁) и y = |y| ⋅ (cos φ₂ + i ⋅ without φ₂), then you can divide them according to the formula below:

Example 2

Find the quotient of complex numbers: x = 4 ⋅ (cos 60° + i ⋅ without 60 °) и y = 2 ⋅ (cos 25° + i ⋅ without 25 °).

Decision:

|x| : |and| = 4 : 2 = 2

φ₁ –φ₂ = 60° – 25° = 35°

x : y = 2 ⋅ (cos 35° + i ⋅ without 35 °)