Difference of squares: formula and examples

In this publication, we will consider the abbreviated multiplication formula, with which you can factorize the difference of squares into factors. We will also analyze examples of solving problems to consolidate the material presented.

Difference of squares formula

Difference of squares of numbers/expressions a и b is equal to the product of their sum and their difference.

a² – b² = (a – b)(a + b)

The formula can be presented from right to left:

(a – b)(a + b) = a² – b²

Note: a² – b² ≠ (a – b)²

Proof of the formula

Arithmetic

Let’s check the formula from the reverse, i.e. multiply (ab) и (a+b).

Opening the brackets, taking into account the rules of arithmetic, we obtain the original formula:

(ab)(a+b) = a² + ab – ba – b² = A² – b².

Geometric

Draw a square with side length a, whose area is a². It contains a smaller square with a side b and area b².

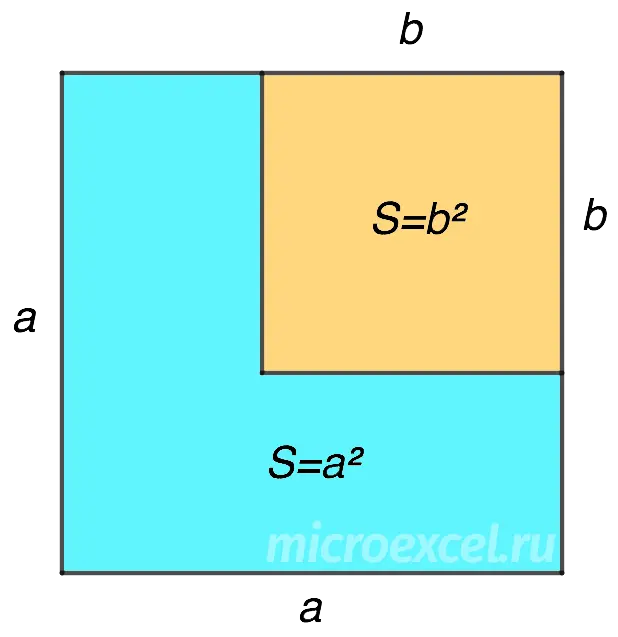
The task is to find the area of ​​the blue figure (a² – b²).

Continuing any of the lines of the sides of the smaller square to the boundaries of the larger one, we get:

• square area b²;
• rectangle with sides a and (ab);
• rectangle with sides b and (ab).

We only need the sum of the areas of the rectangles, which is calculated like this:

S = a ⋅ (a – b) + b ⋅ (a – b) = a² – ab + ba – b² = A² – b²

Examples of tasks

Task 1

Open parenthesis: (8x – 3y)(8x + 3y).

Solution

Let’s apply the abbreviated multiplication formula:

(8x – 3y)(8x + 3y) = 64x² – 9 and²

Task 2

Factor the expression: 25x² – Y².

Solution

Let’s use the formula in reverse:

25x² – Y² = (5x – y)(5x + y)

inspection

(5x – y)(5x + y) = 25x² + 5xy – 5xy – y² = 25x² – Y²