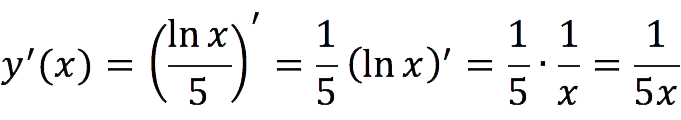Contents
In this publication, we will consider the derivatives of logarithmic functions, as well as analyze examples of solving problems to consolidate the material.
Types of logarithms
Before moving on to the formulas for derivatives, we recall that there are separate names for some logarithms:
1. Decimal logarithm (lg x)
lg x = log10x
Those. is the logarithm of the number x base 10.
2. Natural logarithm (ln x)
ln x = loge x
Those. is the logarithm of the number x by reason e (exhibitor).
General formula for the derivative of the logarithm
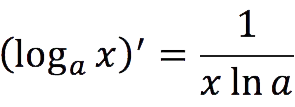
Derivative of the logarithm x by reason a equals the number 1divided by the product of the natural logarithm a and numbers x.
Derivative of the natural logarithm
![]()
Derivative of the natural logarithm of a number x equals one divided by x.
This formula is derived as follows:
![]()
reduction ln e in this case, it is possible due to the property of the logarithm:
![]()
Derivative of the natural logarithm of a complex function u = u (x):
![]()
Examples of tasks
Exercise 1:
Find the derivative of a function y(x) = log4x.
Decision:
Using the general derivative formula, we obtain:
![]()
Exercise 2:
Compute Function Derivative y = ln x / 5.
Decision:
We apply the property of the derivative, according to which the constant can be taken out of the sign of the derivative, and then we use the formula for the natural logarithm: