Derivative of a function: rules and formulas for differentiation

In this publication, we will consider the rules and formulas for differentiating the derivative of functions, and also, we will analyze examples to consolidate the studied material.

Suppose we are given two functions f(x) и u (x), which have derivatives at the point x. Then the following formulas are valid for them:

1. Constant in the derivative

(c ⋅ f(x))‘ = c ⋅ f ‘(X)Where c – a constant

Those. the constant can be taken out of the sign of the derivative.

For example: (5x .)³)‘ = 5 ⋅ (x³)‘

2. Derivative of sum/difference

(f(x) ± u(x))‘ = f ‘(x) ± u ‘(X)

The derivative of the sum/difference of two functions is equal to the sum/difference in which the terms are the derivatives of these functions.

For example: (6x + x²)‘ = (6x)‘ + (x²)‘

3. Derivative of a product

(f(x) ⋅ u(x))‘ = f ‘(x) ⋅ u(x) + f(x) ⋅ u ‘(X)

The derivative of the product of two functions is equal to the sum in which:

• the first term is the product of the derivative of the first function by the second;
• the second term is the opposite.

For example: (ln x ⋅ x³)‘ = (ln x)‘ ⋅ x³ + ln x ⋅ (x³)‘

4. Derivative of the quotient

The derivative of dividing one function by another is found by the following formula:

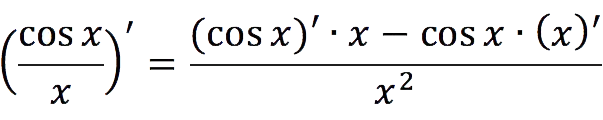
For example:

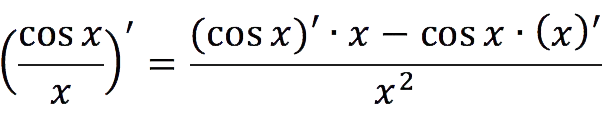
5. Derivative of a complex function

Let’s say the derivative of the function y = y(f) is at the point f₀ = f(x₀), and the functions f = f(x) – at the point x₀.

The derivative of a complex function in this case is:

[y(f(x))]‘ = y ‘(f) ⋅ f ‘(X)

• the multiplicand is the derivative of the given function with respect to the intermediate argument f;
• multiplier is the derivative of the intermediate argument f with respect to the main argument x.