Definition and properties of the median of an equilateral triangle

In this article, we will consider the definition and properties of the median of an equilateral triangle, as well as analyze examples of solving problems to consolidate the material presented.

Definition of the median

Median is a line segment that connects the vertex of the triangle and the midpoint of the opposite side.

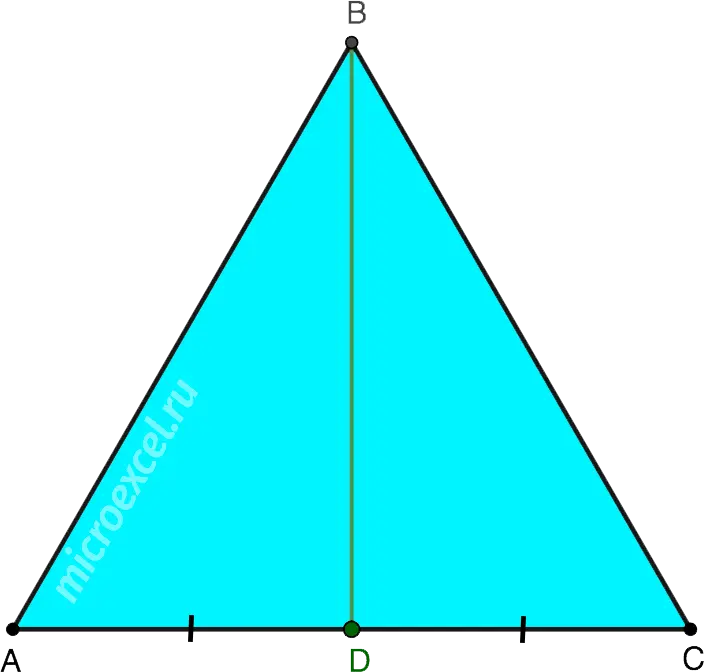
• BD is the median drawn to the side AC;
• AD = DC.

The triangle is called equilateralif all its sides are equal (AB = BC = AC).

Properties of the median of an equilateral triangle

Property 1

Any median in an equilateral triangle is at the same time the height, the perpendicular bisector, and the bisector of the angle from which it is drawn.

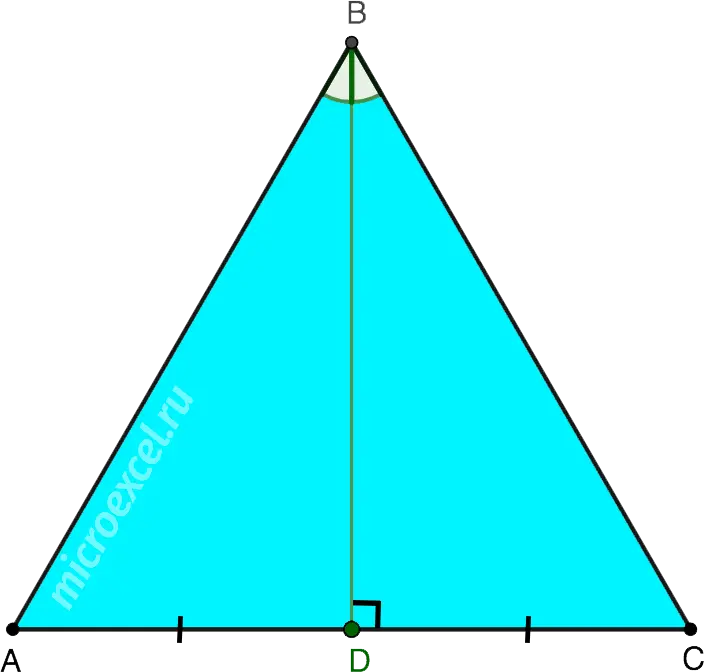
• BD – median, height and perpendicular bisector to the side AC, as well as the angle bisector ABC;
• ∠ABD = ∠CBD.

Property 2

All three medians in an equilateral triangle are equal. Those. AF = BD = CE.

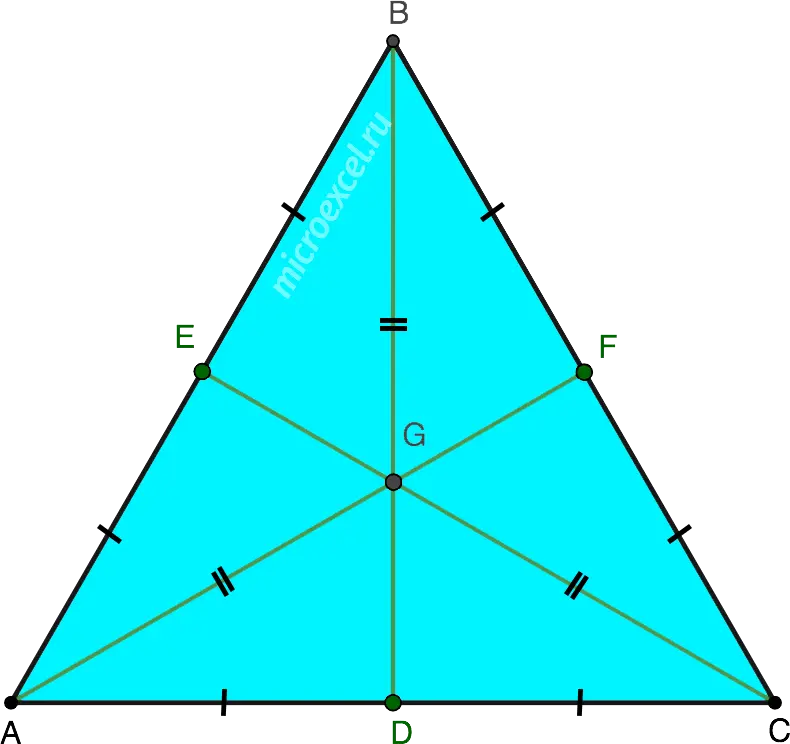
Property 3

Medians in an equilateral triangle intersect at one point, which divides them in a ratio of 2:1.

• G is the center of gravity (centroid) of the triangle;
• AG = 2GF;
• BG = 2GD;
• CG = 2GE.

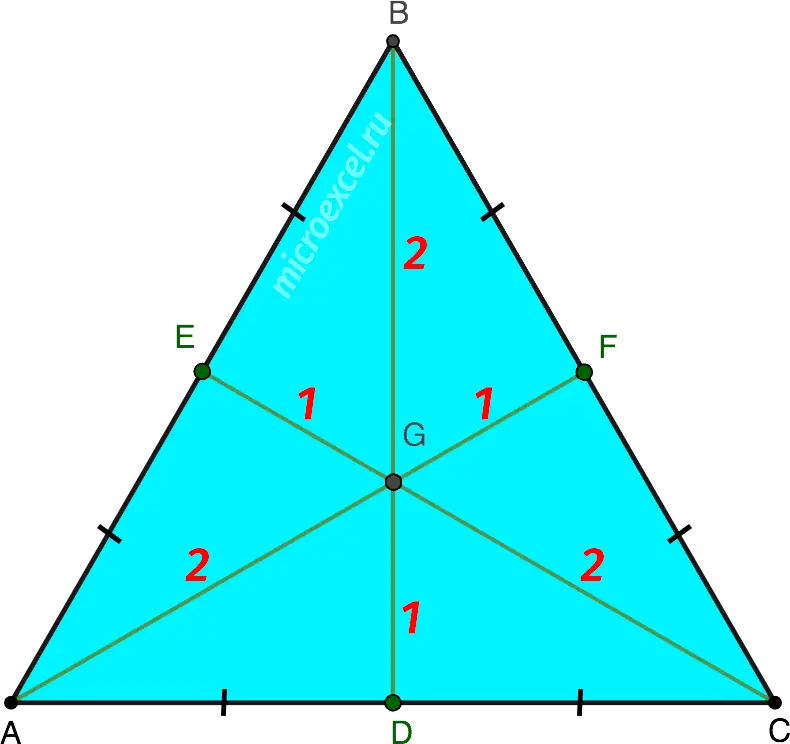
Property 4

Any median of an equilateral triangle divides it into two equal-area (equal-area) right-angled triangles. Those. S₁ = S₂.

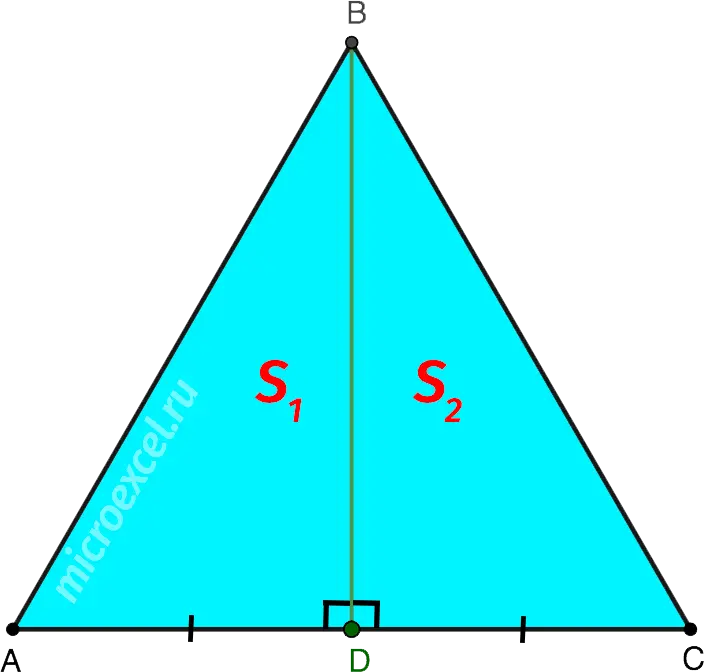
Property 5

An equilateral triangle is divided by three medians into six equal right triangles. Those. S₁ = S₂ = S₃ = S₄ = S₅ = S₆.

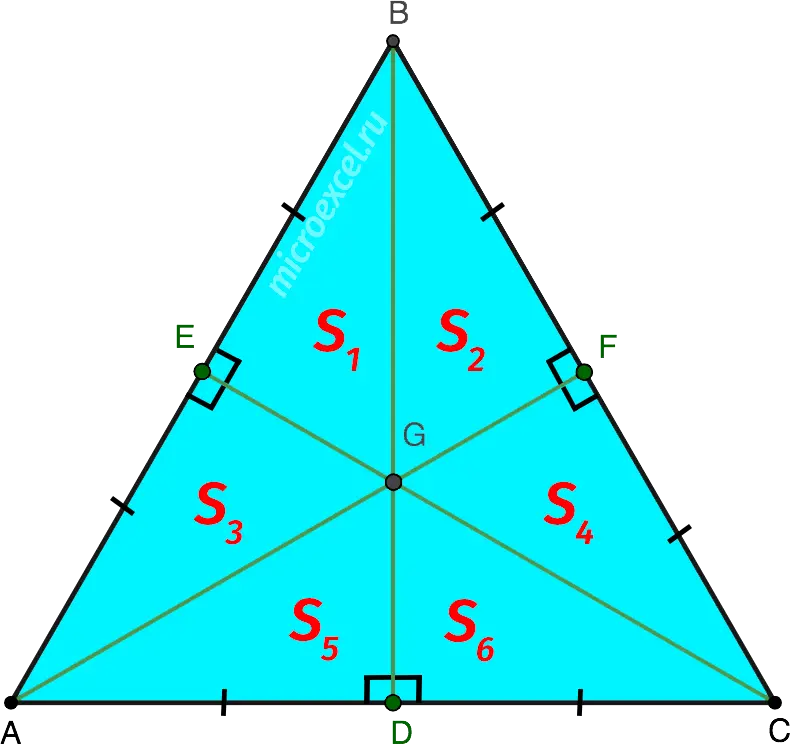
Property 6

The intersection point of the medians in an equilateral triangle is the center of the inscribed and circumscribed circles.

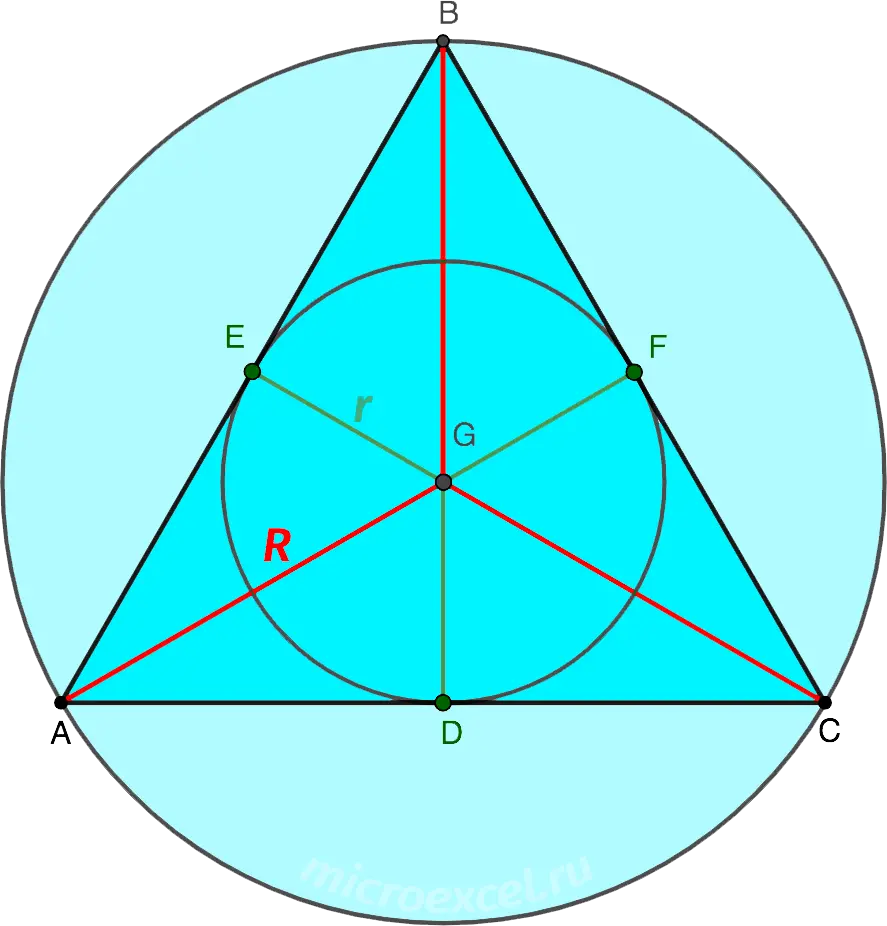
• r is the radius of the inscribed circle;
• R is the radius of the circumscribed circle;
• R = 2r (follows from Properties 3).

Property 7

The length of the median of an equilateral triangle can be calculated using the formula:

a is the side of the triangle.

Examples of tasks

Task 1

Calculate the length of the median of an equilateral triangle if its side is known to be 6 cm.

Solution

To find the required value, apply the formula above:

Task 2

The largest side of one of the triangles formed as a result of the intersection of three medians in an equilateral triangle is 8 cm. Find the length of the side of this triangle.

Solution

Let’s draw a drawing according to the conditions of the problem.

Of Properties 5 we know that as a result of the intersection of all medians, 6 right triangles are formed.

• BG = 8 cm (the largest side, is the hypotenuse △BFG);
• FG = 4 cm (leg △BFG, 2 times less than the hypotenuse BG – follows from Properties 3).

We use to find the length of the second leg BF:

BF² = BG² – FG² = 8² – 4² = 48 cm².

Consequently, the BF ≈ 6,93 cm.

BF equals half a side BC (since the median bisects the side of the triangle), therefore, BC ≈ 13,86 cm.