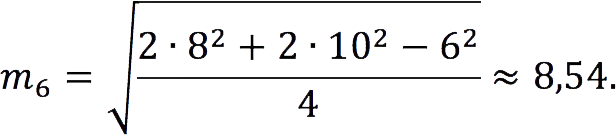Contents
In this article, we will consider the definition of the median of a triangle, list its properties, and also analyze examples of solving problems to consolidate theoretical material.
Definition of the median of a triangle
Median is a line segment that connects a vertex of a triangle with the midpoint of the side opposite that vertex.
- BF is the median drawn to the side AC.
- AF = FC
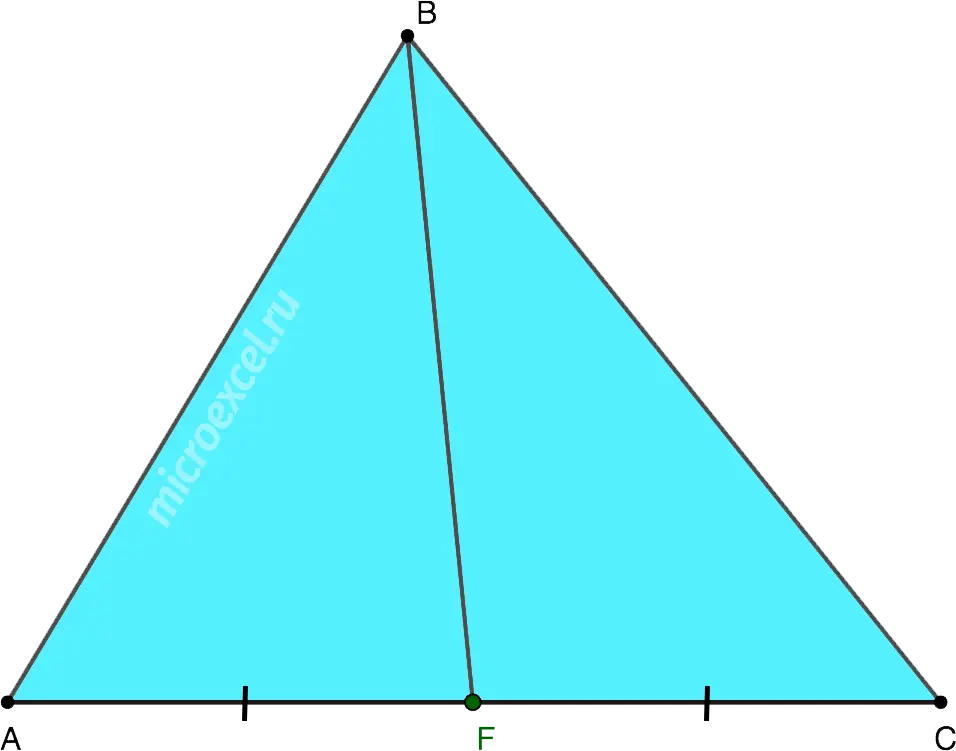
Base median – the point of intersection of the median with the side of the triangle, in other words, the midpoint of this side (point F).
median properties
Property 1 (main)
Because If a triangle has three vertices and three sides, then there are three medians, respectively. They all intersect at one pointO), which is called centroid or center of gravity of a triangle.
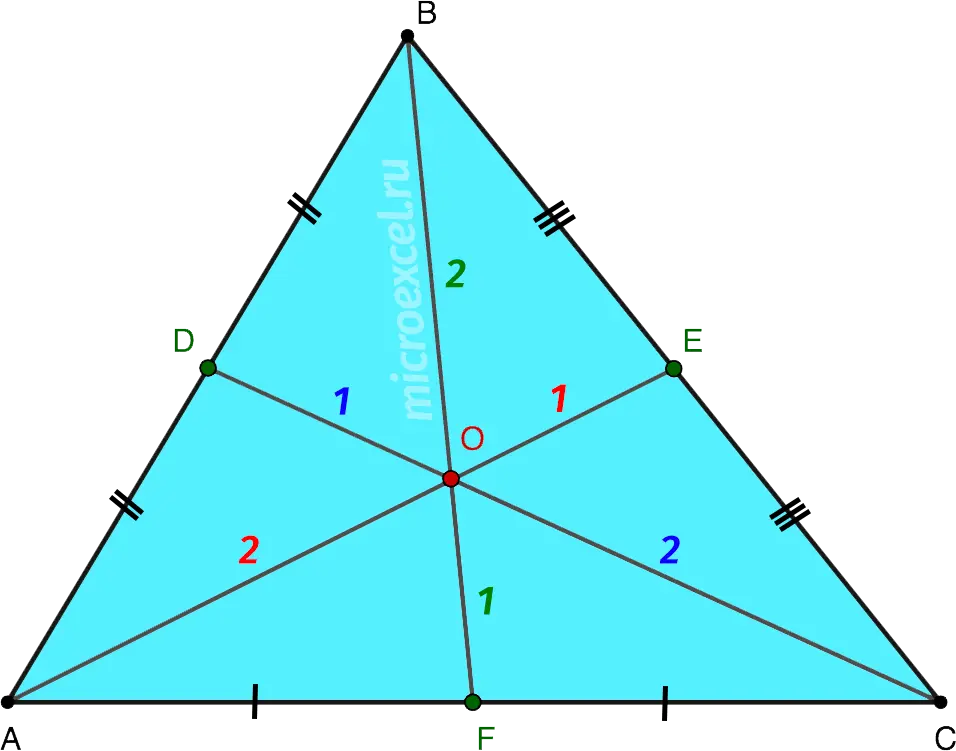
At the point of intersection of the medians, each of them is divided in a ratio of 2: 1, counting from the top. Those.:
- AO = 2OE
- BO = 2OF
- CO = 2OD
Property 2
The median divides the triangle into 2 triangles of equal area.
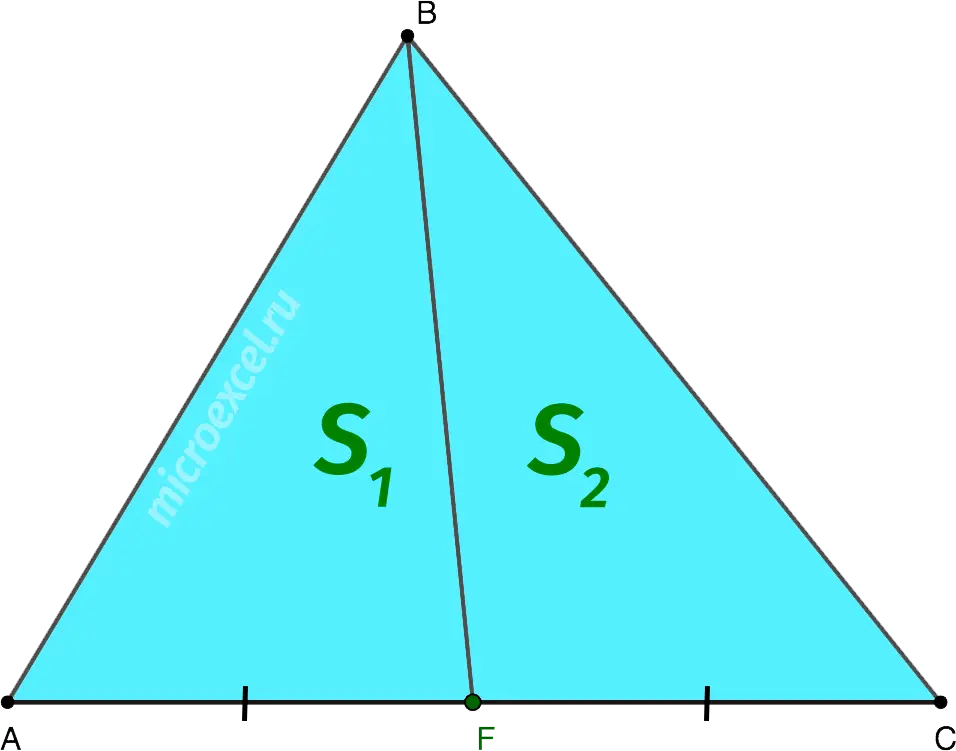
S1 = S2
Property 3
Three medians divide the triangle into 6 triangles of equal area.
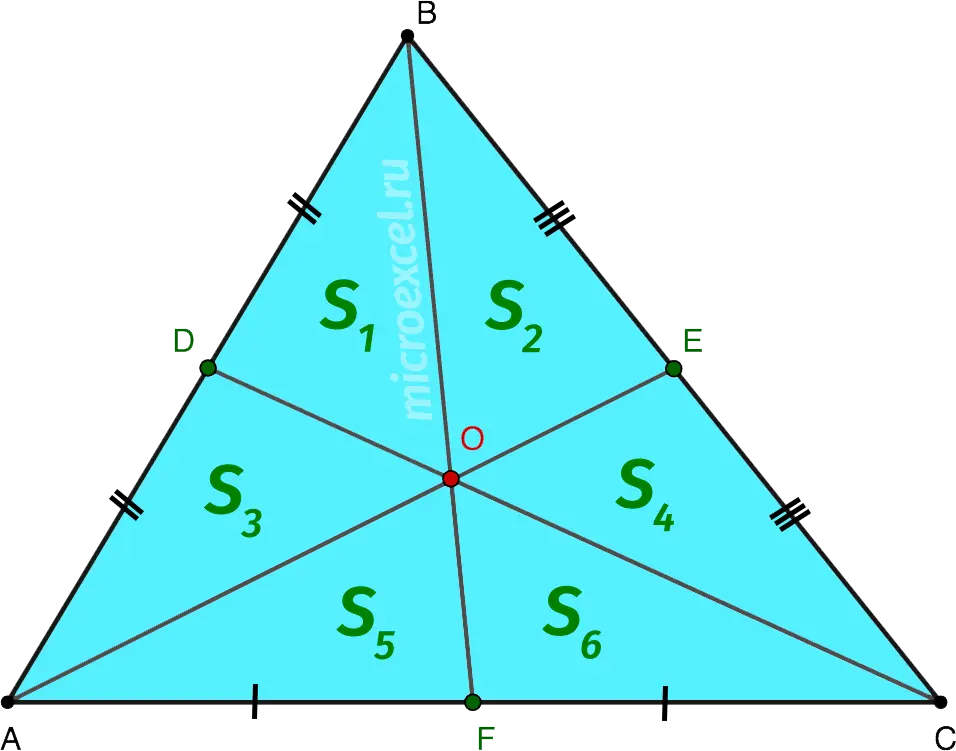
S1 = S2 = S3 = S4 = S5 = S6
Property 4
The smallest median corresponds to the largest side of the triangle, and vice versa.
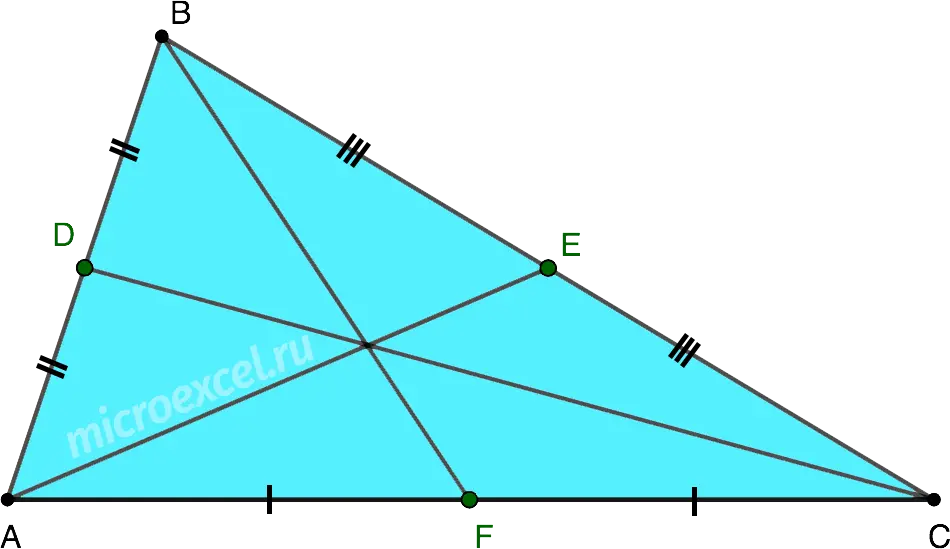
- AC is the longest side, hence the median BF – the shortest.
- AB is the shortest side, hence the median CD – the longest.
Property 5
Suppose we know all the sides of the triangle (let’s take them as a, b и c).
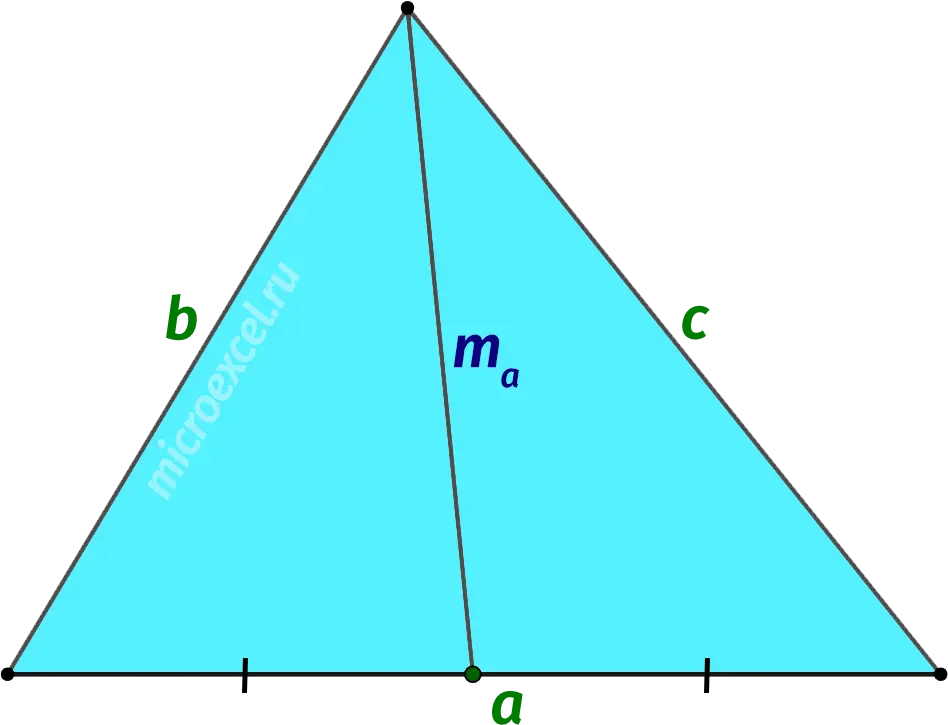
median length madrawn to the side a, can be found by the formula:
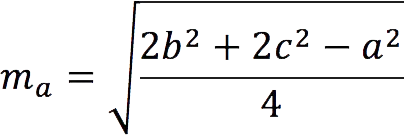
Examples of tasks
Task 1
The area of one of the figures formed as a result of the intersection of three medians in a triangle is 5 cm2. Find the area of the triangle.
Solution
According to property 3, discussed above, as a result of the intersection of three medians, 6 triangles are formed, equal in area. Consequently:
S△ = 5 cm2 ⋅ 6 = 30 cm2.
Task 2
The sides of the triangle are 6, 8 and 10 cm. Find the median drawn to the side with a length of 6 cm.
Solution
Let’s use the formula given in property 5: