Definition and properties of the median of a right triangle

In this article, we will consider the definition and properties of the median of a right triangle drawn to the hypotenuse. We will also analyze an example of solving a problem to consolidate the theoretical material.

Determining the median of a right triangle

Median is the line segment that connects the vertex of the triangle to the midpoint of the opposite side.

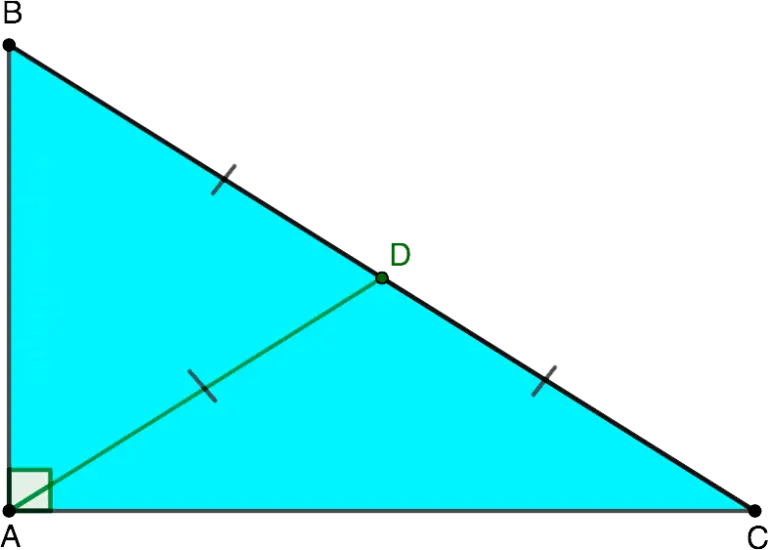
Right triangle is a triangle in which one of the angles is right (90°) and the other two are acute (<90°).

Properties of the median of a right triangle

Property 1

Median (AD) in a right triangle drawn from the vertex of the right angle (∠LAC) to the hypotenuse (BC) is half the hypotenuse.

• BC = 2AD
• AD = BD = DC

Consequence: If the median is equal to half of the side to which it is drawn, then this side is the hypotenuse, and the triangle is right-angled.

Property 2

The median drawn to the hypotenuse of a right triangle is equal to half the square root of the sum of the squares of the legs.

For our triangle (see the figure above):

It follows from and Properties 1.

Property 3

The median dropped on the hypotenuse of a right triangle is equal to the radius of the circle circumscribed around the triangle.

Those. BO is both the median and the radius.

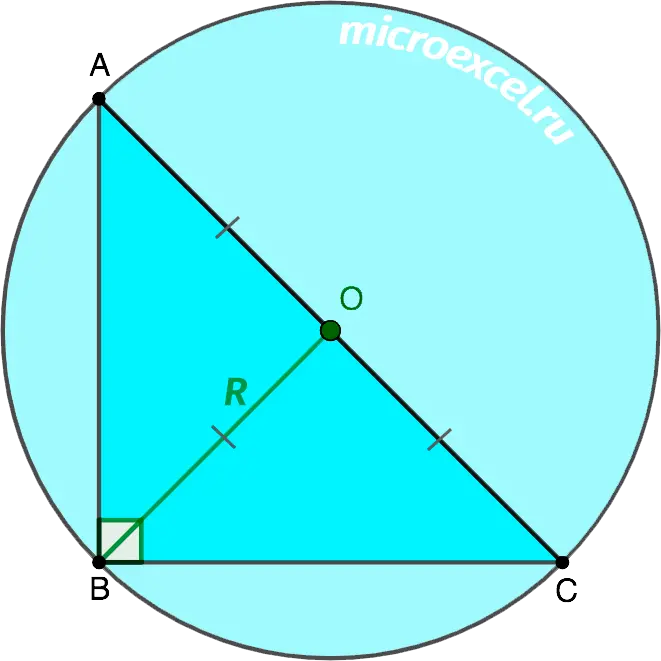
Note: Also applicable to a right triangle, regardless of the type of triangle.

Example of a problem

The length of the median drawn in the hypotenuse of a right triangle is 10 cm. And one of the legs is 12 cm. Find the perimeter of the triangle.

Solution

The hypotenuse of a triangle, as follows from Properties 1, twice the median. Those. it equals: 10 cm ⋅ 2 = 20 cm.

Using the Pythagorean theorem, we find the length of the second leg (we take it as “B”, the famous leg – for “to”, hypotenuse – for “with”):

b² = c² – and² = 20² – 12² = 256.

Consequently, the b = 16 cm.

Now we know the lengths of all sides and we can calculate the perimeter of the figure:

P_△ = 12 cm + 16 cm + 20 cm = 48 cm.