Contents
In this article, we will consider the definition and properties of medians drawn to the base and sides of an isosceles triangle, and also analyze an example of solving a problem to consolidate theoretical material.
Definition of the median
median A line segment in a triangle that connects the vertex and the midpoint of the opposite side is called.
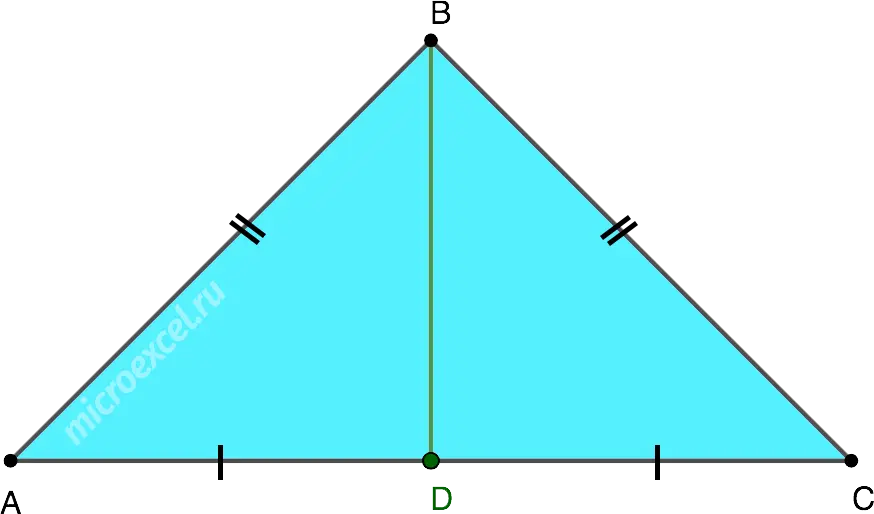
- BD – median △ABC;
- AD = DC.
Triangle is isosceles, if two of its sides are equal (lateral), and the third side is the base of the figure.
- AB = BC – sides;
- AC – reason.
Properties of the median in an isosceles triangle
Property 1
The median in an isosceles triangle, drawn to the base, is both the height lowered to the base and the bisector of the angle from which it is drawn.
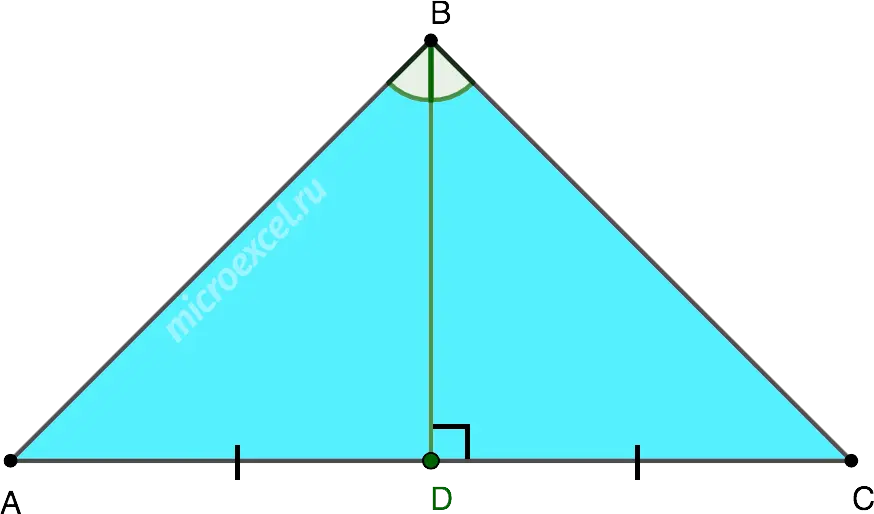
- BD – median and height lowered to the base AC, as well as the angle bisector ABC.
- ∠ABD = ∠CBD
Property 2
In an isosceles triangle, the medians intersect at one point (the center of gravity) and divide at this point in a ratio of 2:1.
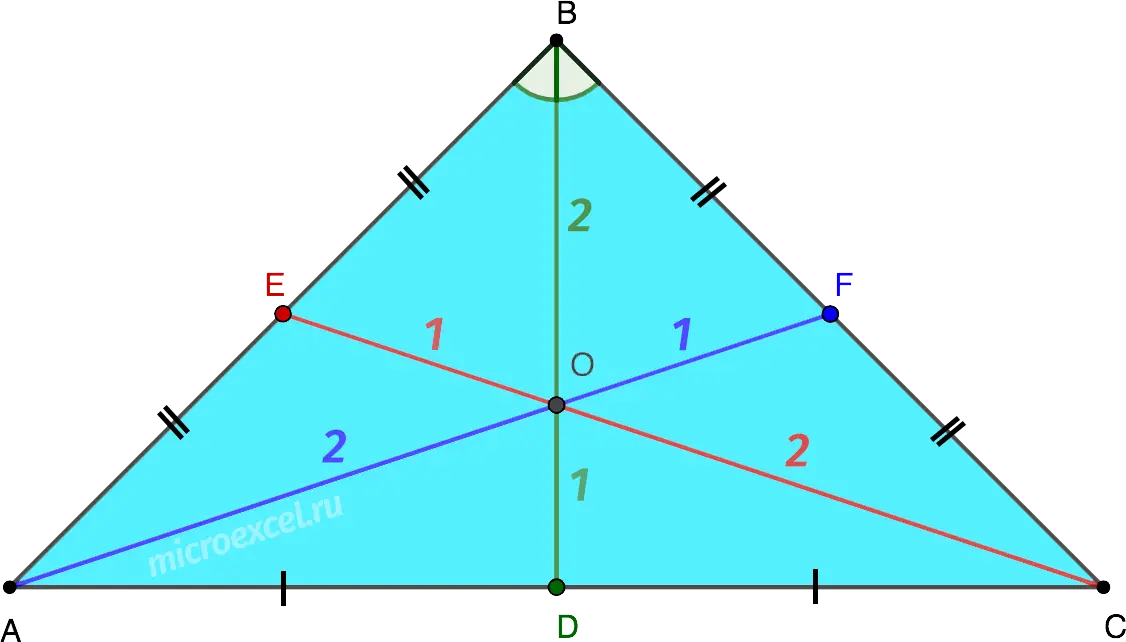
- O is the center of gravity or centroid of the triangle;
- AO = 2OF;
- BO = 2OD;
- CO = 2OE.
Property 3
The median divides an isosceles triangle into 2 triangles of equal area. Consequently, S1 = S2.
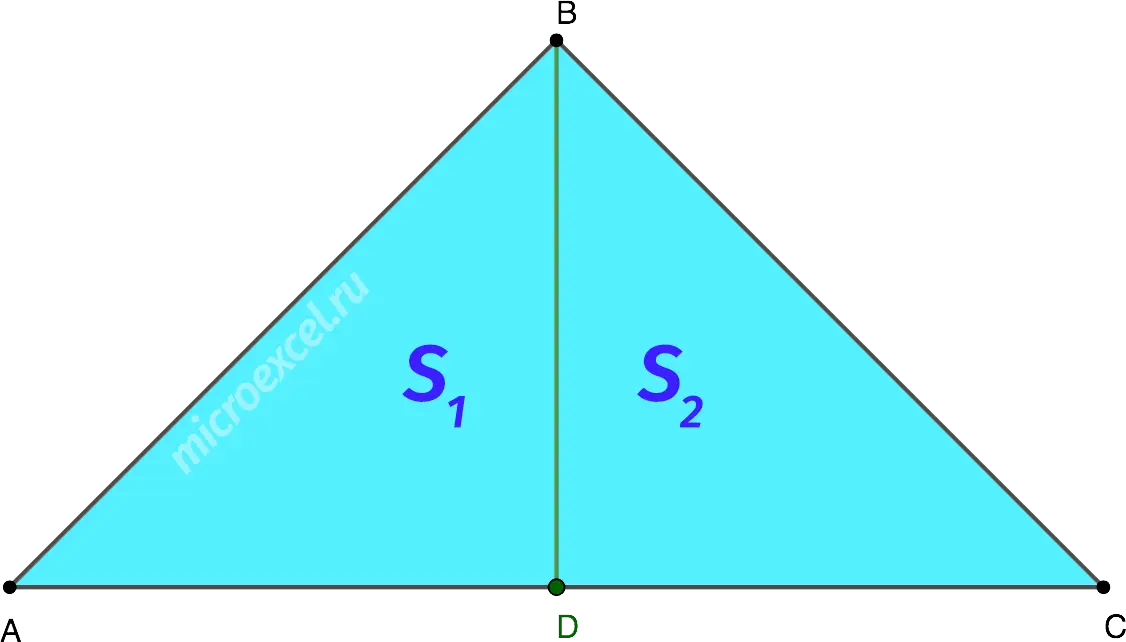
Property 4
If you draw three medians in an isosceles triangle, 6 equal triangles are formed (S1 = S2 = S3 = S4 = S5 = S6).
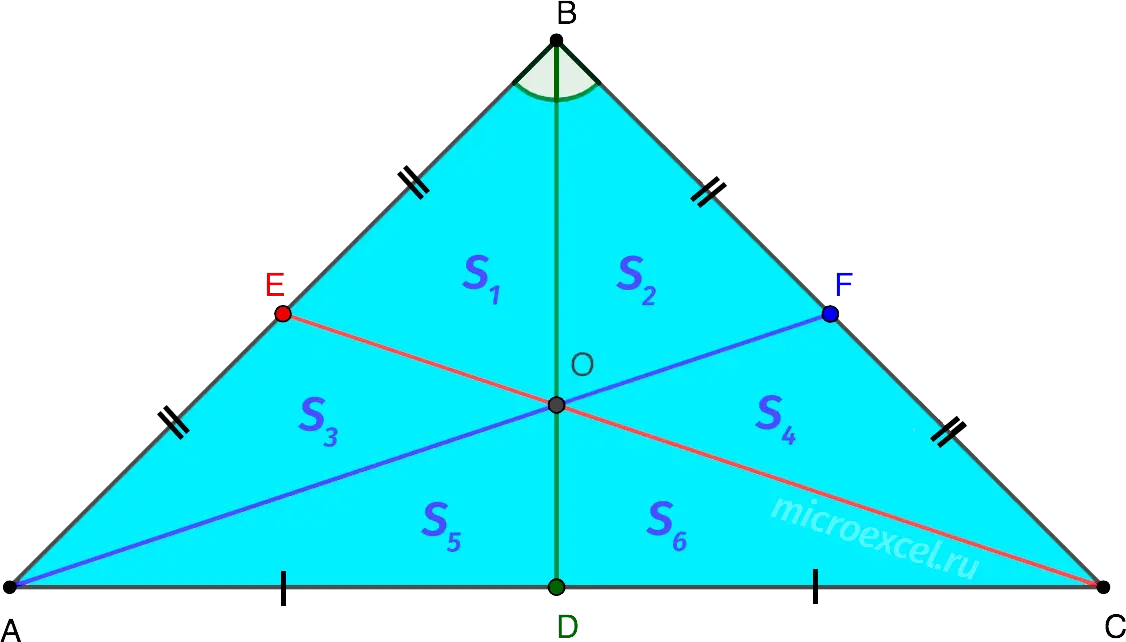
Property 5
The length of the median in an isosceles triangle drawn to the base can be found using the following formula:
![]()
- a – reason;
- b – side.
Property 6
This property, unlike those listed above, does not apply to the median lowered to the base of the figure. It says:
The medians drawn to the sides of an isosceles triangle are equal to each other.
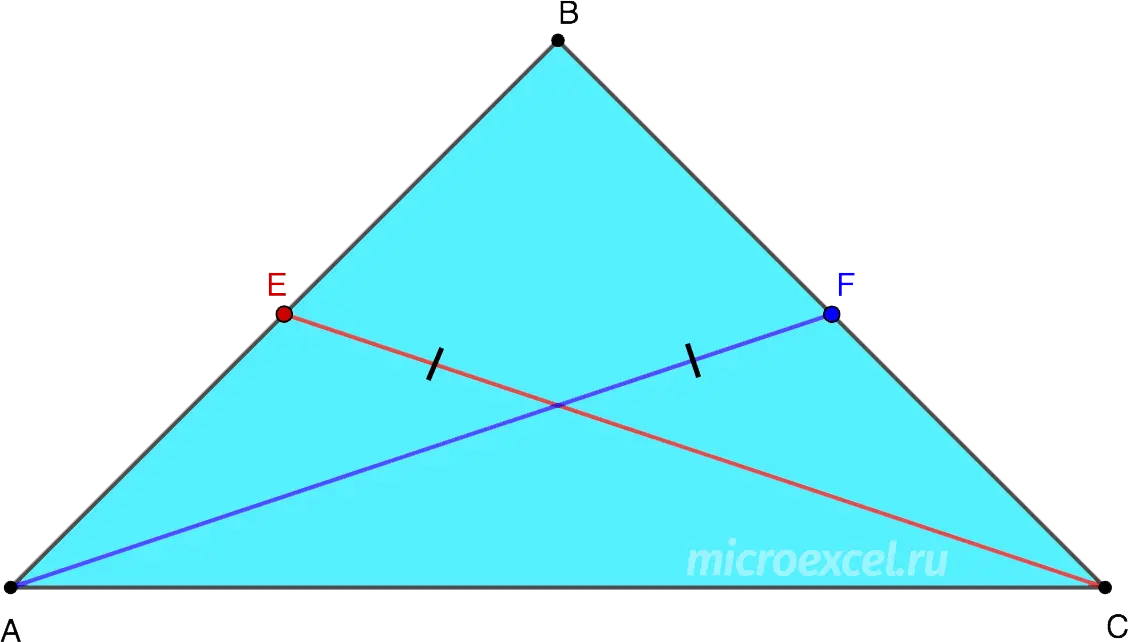
AF = CE, Consequently, AE = EB = BF = FC.
Example of a problem
The base of an isosceles triangle is 7 cm, and the side is 12 cm. Find the length of the median drawn to the base of the figure.
Solution
Let’s use the formula presented in Property 5, substituting into it the values known to us according to the conditions of the problem:
![]()









