Contents
In this publication, we will consider determining the height of a triangle, demonstrate how it looks depending on the type of triangle, and also list its main properties.
Determining the Height of a Triangle
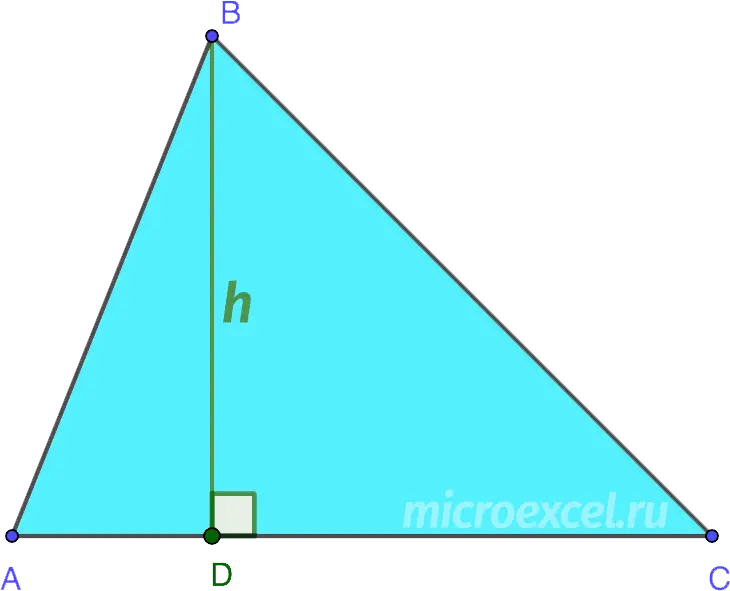
Height of triangle – this is a perpendicular that is lowered from the top of the figure to the opposite side.
height base – a point on the opposite side of the triangle, which is crossed by the height (or the point of intersection of their extensions).
Height is usually denoted by the letter h (sometimes like ha – this means that it is held to the side a).
Height in different types of triangles
Depending on the type of figure, the height can be:
- pass inside the triangle (in acute-angled △);

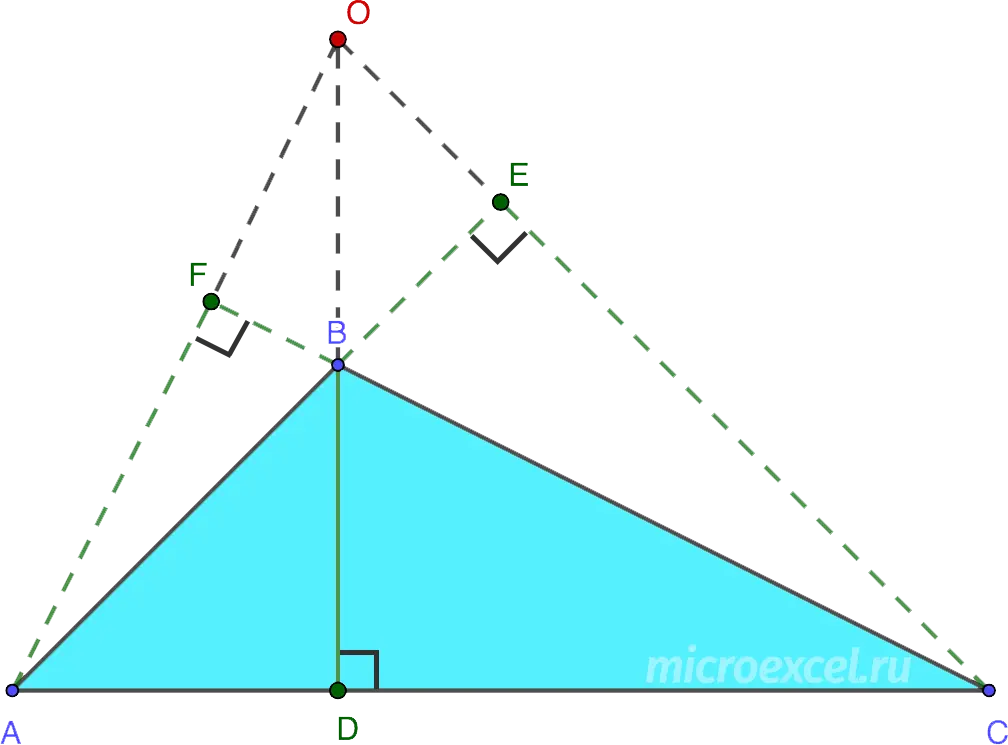
- pass outside the triangle (in an obtuse △);

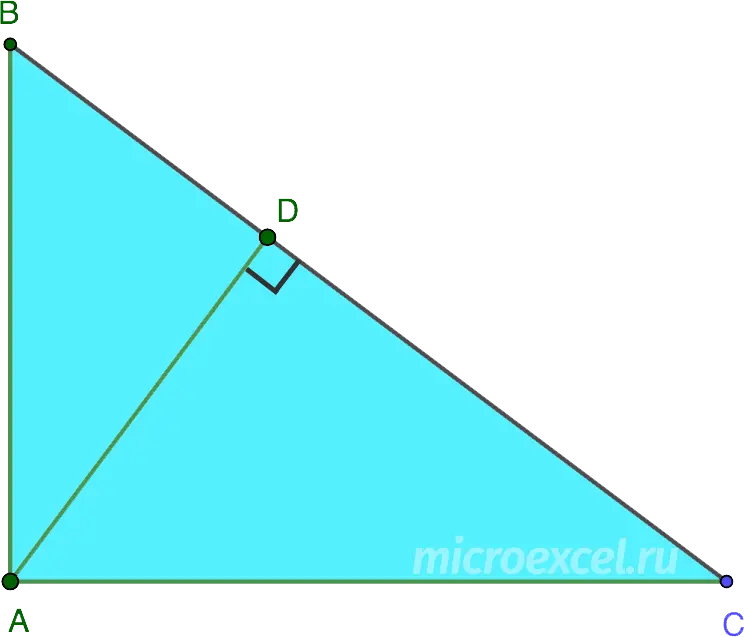
- be one of the legs (in a rectangular △), except for the height drawn to the hypotenuse.

Triangle Height Properties
Property 1
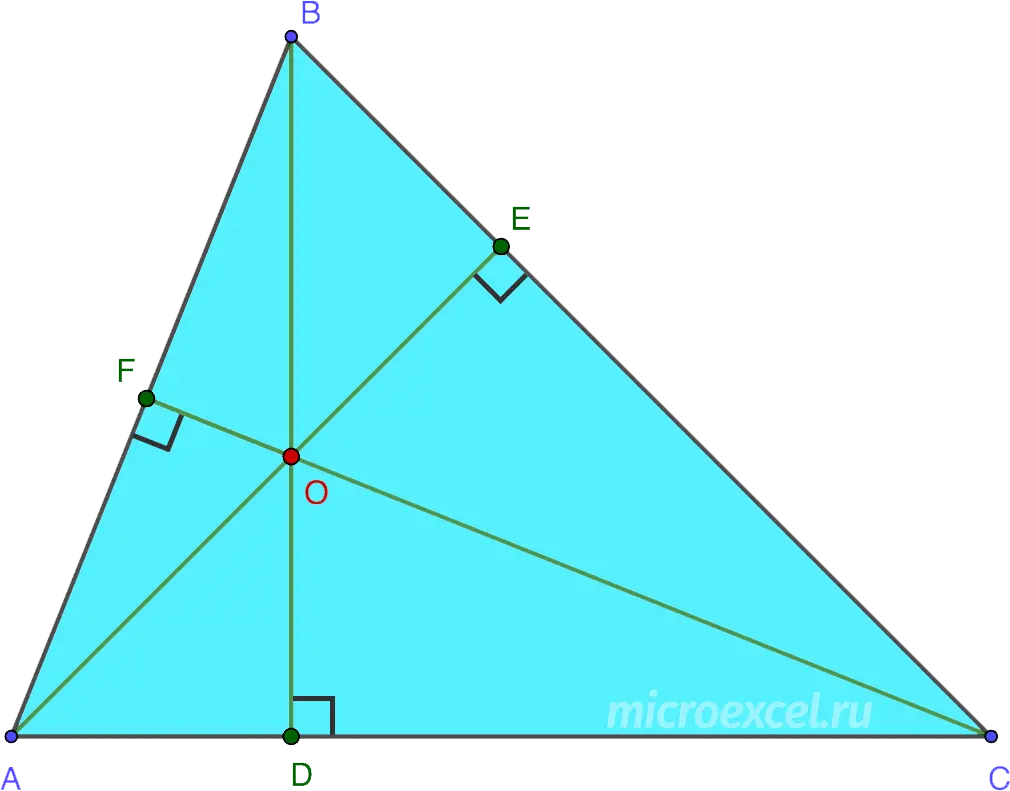
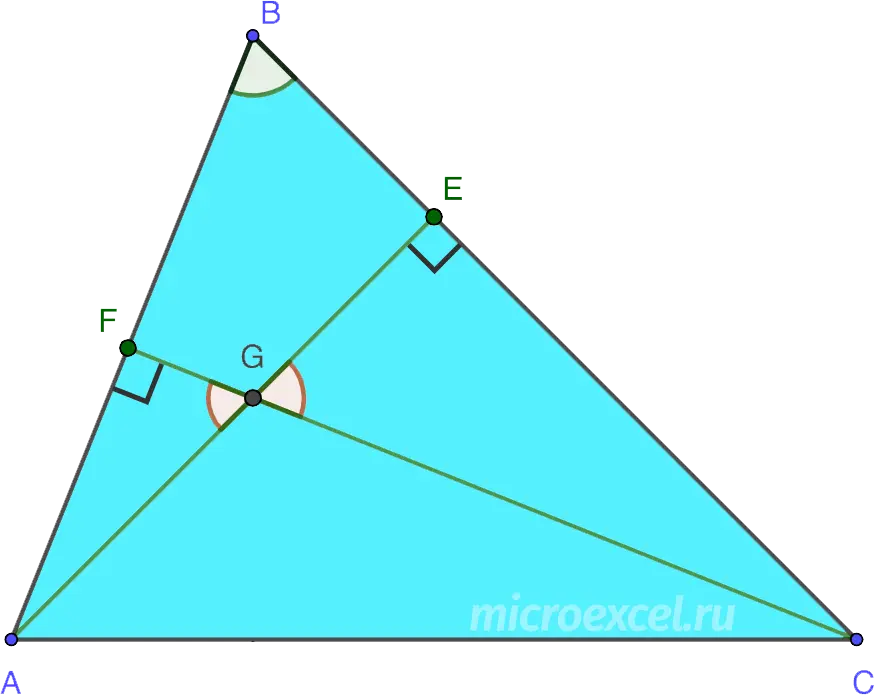
All three heights in a triangle (or their extensions) intersect at one point, which is called orthocenter (dot O in the drawings below).
- in an acute triangle;

- in an obtuse triangle;

- in a right triangle.

Vertex A is, among other things, the point of intersection of heights.
Property 2
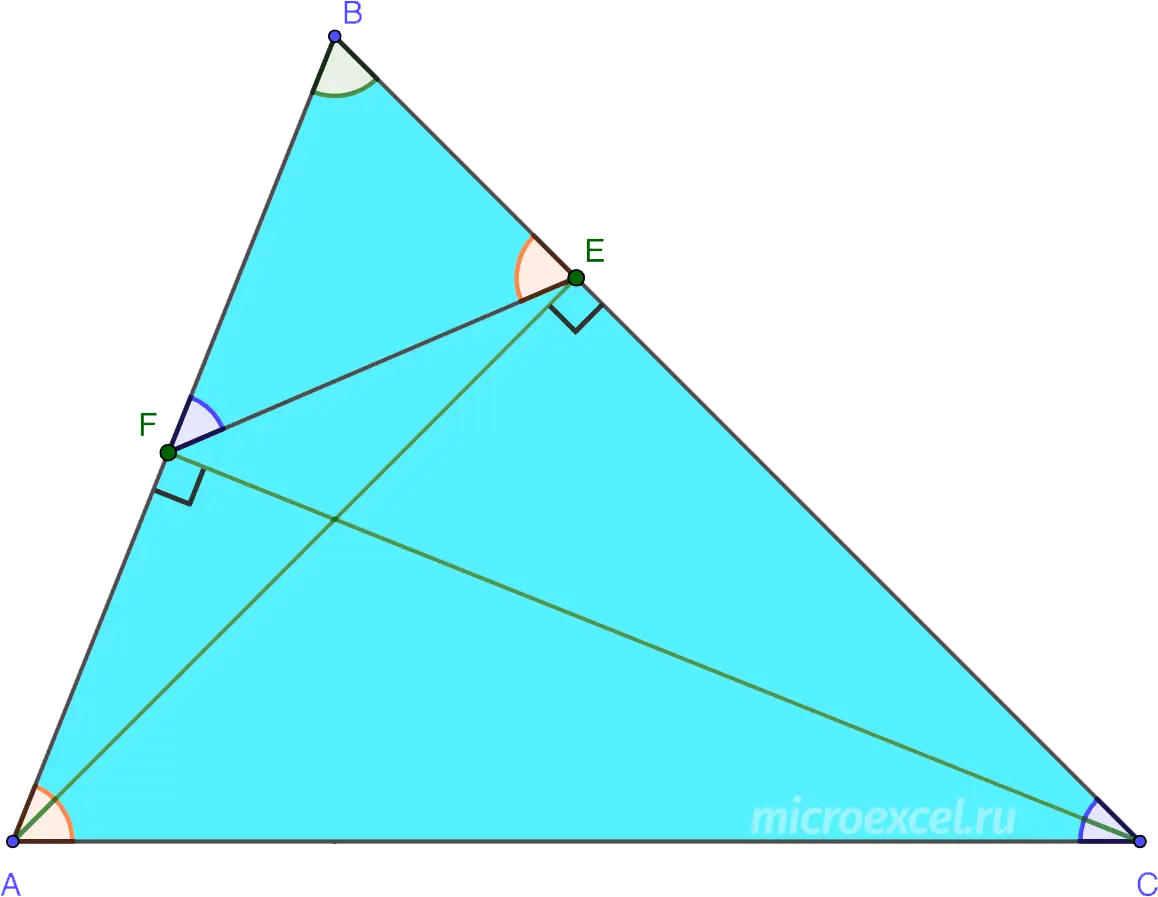
When two heights intersect in a triangle, the following similar triangles are formed:
- △ABE∼△CBF: two corners (∠ABC – general, ∠General Conditions of Purchase and ∠SFBC are straight).

- △AFG∼△CEG: two corners (∠AFG and ∠CEG – straight lines, ∠AGF and ∠CGE equal as vertical angles).
- △ABC∼△BEF: three equal angles (∠ABC = ∠EBF, ∠ACB = ∠SFOE, ∠CAB = ∠BEF).

Note: the proof of the similarity of the last pair of triangles is quite long and is not the purpose of this article, so we will dwell on it in detail.
Property 3
The intersection point of the heights in an acute triangle is the center of a circle inscribed in it. orthotriangle.
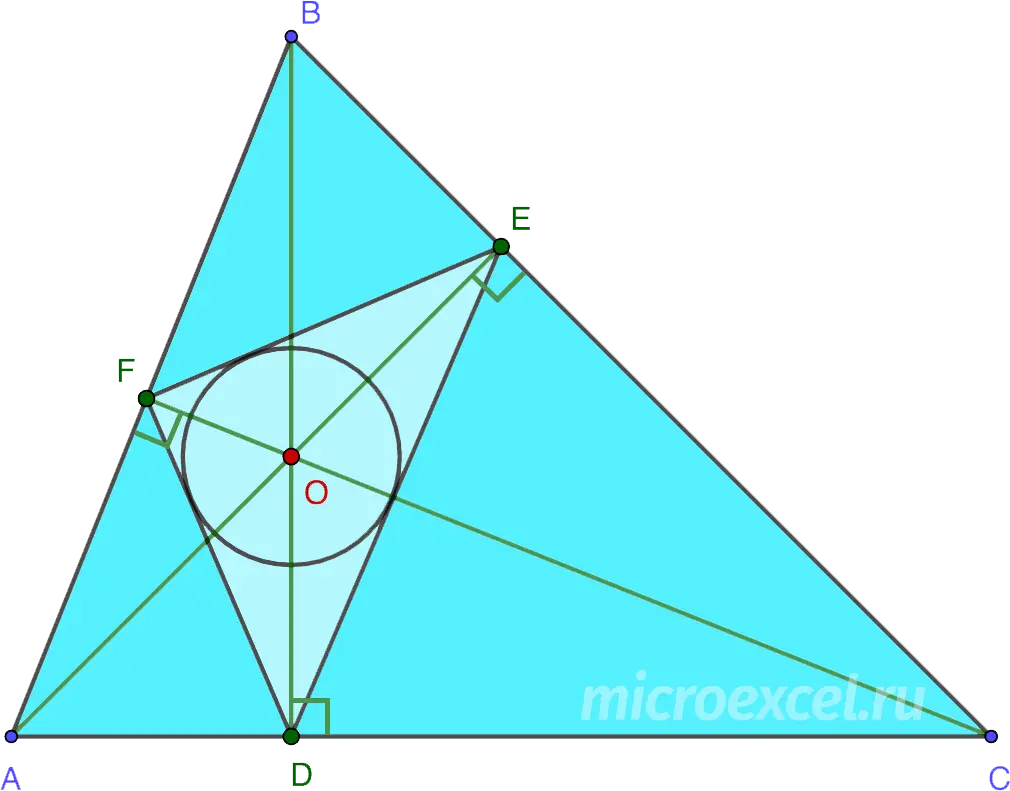
Orthotriangle – a triangle whose vertices are the bases of the heights △ABC. In our case, this is △DEF.
Property 4
Points that are symmetrical to the orthocenter of a triangle with respect to its sides lie on a circle circumscribed around this triangle.

- GE = EL
- GD = DM
- GF = FK
Note: formulas for finding the height of a triangle are discussed in detail in our publication -.