Definition and properties of the angle bisector of a triangle

In this publication, we will consider the definition and basic properties of the bisector of the angle of a triangle, and also give an example of solving the problem in order to consolidate the presented material.

Determining the Bisector of an Angle of a Triangle

Angle bisector is a ray that originates at the vertex of an angle and bisects the given angle.

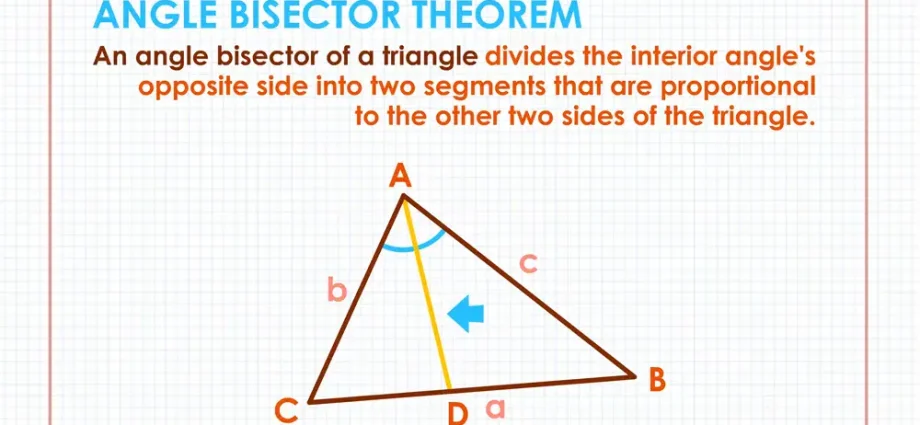
Bisector of a triangle is a segment that connects the vertex of an angle of a triangle with the opposite side and divides this angle into two equal parts. Such a bisector is also called internal.

• BD – angle bisector ABC;
• a = b.

Base of the bisector – a point on the side of the triangle that the bisector intersects. Those. in our case, this is the point D.

External is called the bisector of the angle adjacent to the interior angle of the triangle.

• CD is the outer bisector of the angle adjacent to ∠ACB;
• a = b.

Triangle Bisector Properties

Property 1 (bisector theorem)

The bisector of an angle of a triangle divides its opposite side in a proportion equal to the ratio of the sides adjacent to the given angle. Those. for our triangle (see the topmost figure):

Property 2

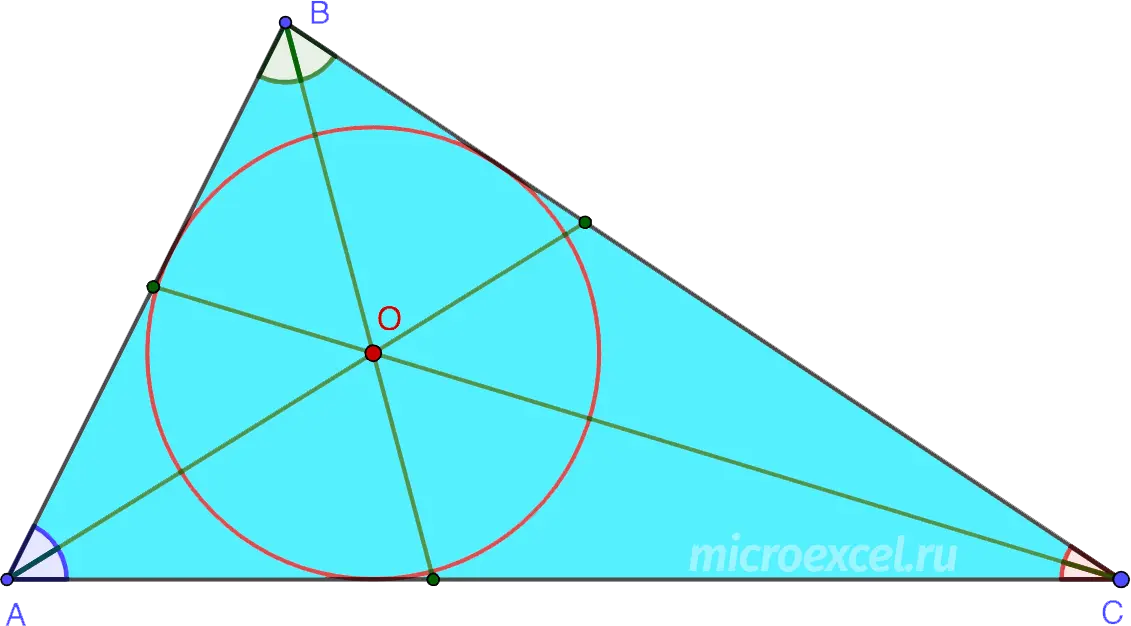
The point of intersection of three internal bisectors of any triangle (called center) is the center of a circle inscribed in the figure.

Property 3

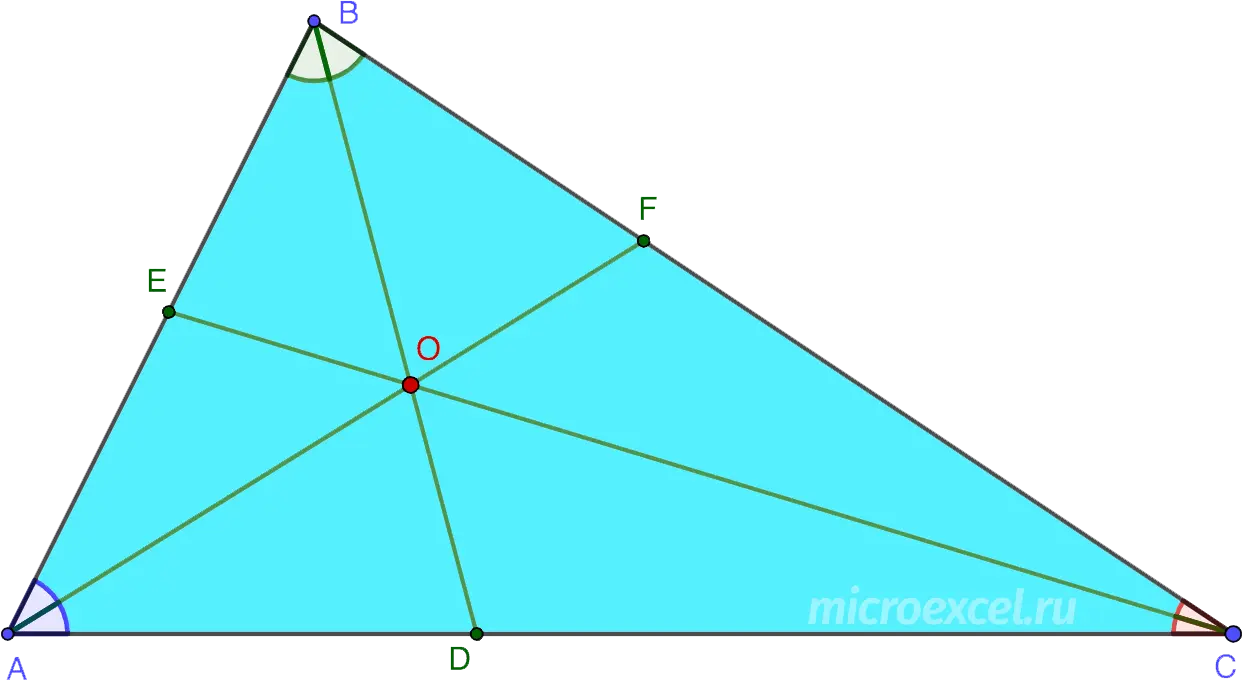
All bisectors of a triangle at the point of intersection are divided in a ratio equal to the sum of the sides adjacent to the angle, divided by the opposite side (counting from the top).

Property 4

If the lengths of the segments formed on the side that the bisector intersects, as well as the other two sides of the triangle, are known, you can find the length of the bisector using the formula below (follows from):

BD² = AB ⋅ BC – AD ⋅ DC

Property 5

The outer and inner bisectors of the same angle of a triangle are perpendicular to each other.

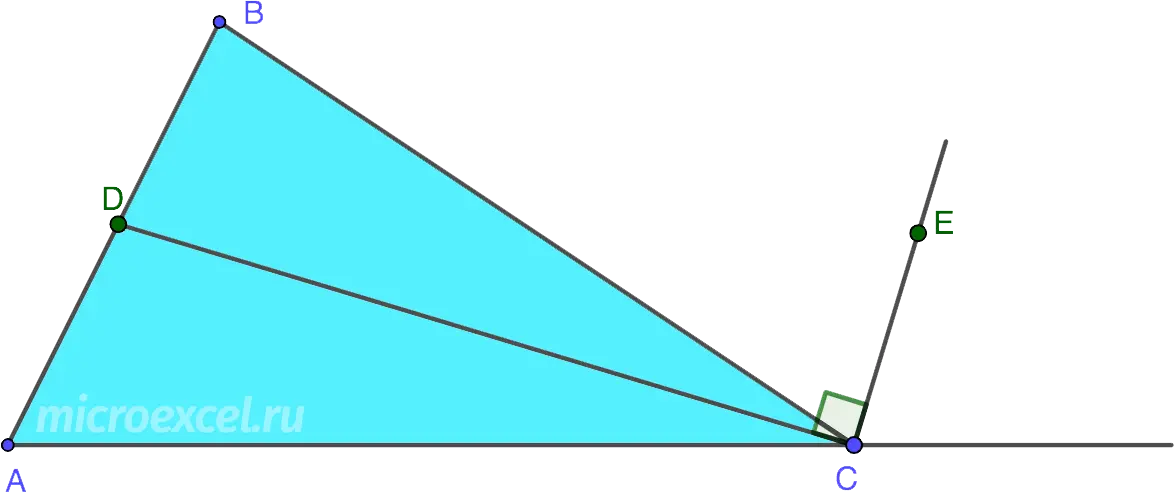
• CD is the internal bisector ∠ACB;
• CE is the bisector of the angle adjacent to ∠ACB;
• ∠DCE equal to 90°, i.e. bisectors CD и CE are perpendicular.

Example of a problem

Given a right triangle with legs 6 cm and 8 cm. Find the length of the bisector drawn to the hypotenuse.

Solution

Let’s draw a drawing according to the conditions of the problem.

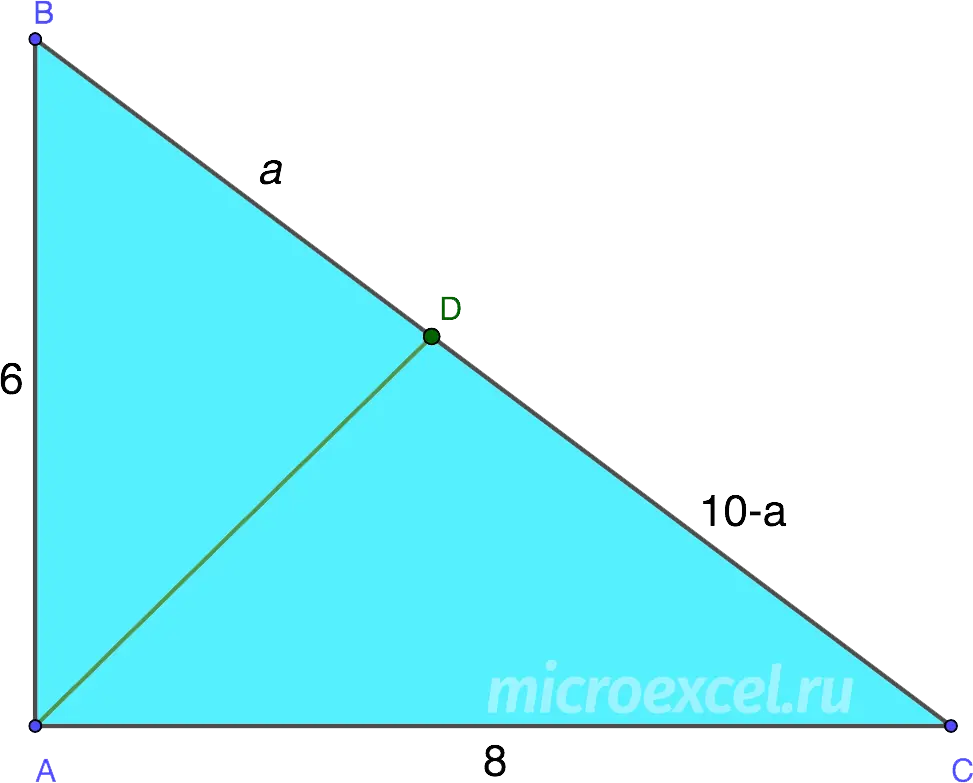
Applying the Pythagorean theorem we can find the length of the hypotenuse (its square is equal to the sum of the squares of the two legs).

BC² =AB² + AC² = 6² + 8² = 100.

Consequently, the BC = 10 cm.

Next, we make a proportion according to Property 1, conditionally accepting the segment BD on the hypotenuse for “a” (then DC = “10-a”):

Get rid of the fractions and solve the resulting equation:

8a = 60 – 6a

14a = 60

a ≈ 4,29

In this way, BD ≈ 4,29 cm, CD ≈ 10 – 4,29 ≈ 5,71 cm.

Now we can calculate the length of the bisector using the formula given in Property 4:

AD² = AB ⋅ AC – BD ⋅ DC = 6 ⋅ 8 – 4,29 ⋅ 5,71 ≈ 23,5.

Consequently, the AD ≈ 4,85 cm.