Contents
In this publication, we will look at how a decimal fraction can be divided into a natural integer or other decimal fraction. We will also analyze examples to consolidate the material presented.
Dividing a decimal fraction by a natural number
Divisor – 10, 100, 1000, 10000, etc.
To divide a decimal fraction into a natural number 10, 100, 1000, 10000, etc., we carry out the transfer of the decimal separator (comma) to the left by as many positions as the divisor contains zeros.
Example 1
62,75: 10 = 6,275
Explanation: There is only one zero in the number 10, so we shift the comma one position to the left.
Example 2
154,39: 100 = 1,5439
Explanation: There are two zeros in the number 100, which means we shift the comma by two positions.
Note: if the number of zeros in the divisor is greater than the number of digits in the integer part of the dividend, then we count as many positions as the fraction allows, then add the remaining number of zeros on the left, put a comma and add zero to the integer part of the new decimal fraction.
Example 3
62,75: 1000 = 0,06275
Explanation: Because there are three zeros in the number 1000, count two positions to the left, add the remaining zero on the left side, write a comma and then zero in the integer part of the resulting fraction.
Divisor – any number
To divide a decimal by any natural integer:
- Ignoring the comma, we perform division by a column, as if the dividend is an integer, not a fraction.
- As soon as the remainder is not divisible by the divisor, put a comma in the quotient. Moreover, if the integer part of the dividend is initially less than the divisor, then the integer part of the new fraction (quotient) will be less than one, i.e. equals 0.
- We continue to perform the division, writing the resulting numbers already in the fractional part of the result. Here, if the remainder cannot be completely divided by the divisor, we simultaneously add zero to the right to it and to the quotient and continue the action until we get a zero remainder (for finite fractions), or until the required number of digits after the decimal point in the quotient is obtained.
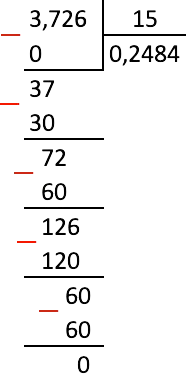
Example 4: Divide the fraction 12,516 by 3.
Decision:
Example 5: Divide the fraction 3,726 by 15.
Decision:
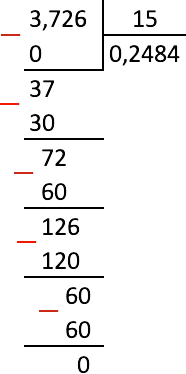
Because the integer part of the original fraction is less than the divisor, which means that the integer part of the quotient is equal to 0 (i.e., we write zero, put a comma and continue to divide).
Division of a decimal by another decimal
To divide one decimal fraction into another, we multiply both fractions by such a number (10, 100, 1000, etc.) so that they become integers (the number of zeros in the multiplier depends on the largest number of digits after the decimal point for a particular fraction) . Then we find the quotient.
Note: the same trick can be used to divide a decimal by an integer.
Example 6: find how much will be 5,468 divided by 3,2.
Decision:
The fraction 5,468 has three digits after the decimal point, while 3,2 has only one. So we multiply them both by 1000, then we find the required result.










