Cross product of vectors

In this publication, we will consider how to find the cross product of two vectors, give a geometric interpretation, an algebraic formula and properties of this action, and also analyze an example of solving the problem.

Geometric interpretation

Vector product of two non-zero vectors a и b is a vector c, which is denoted as [a, b] or a x b.

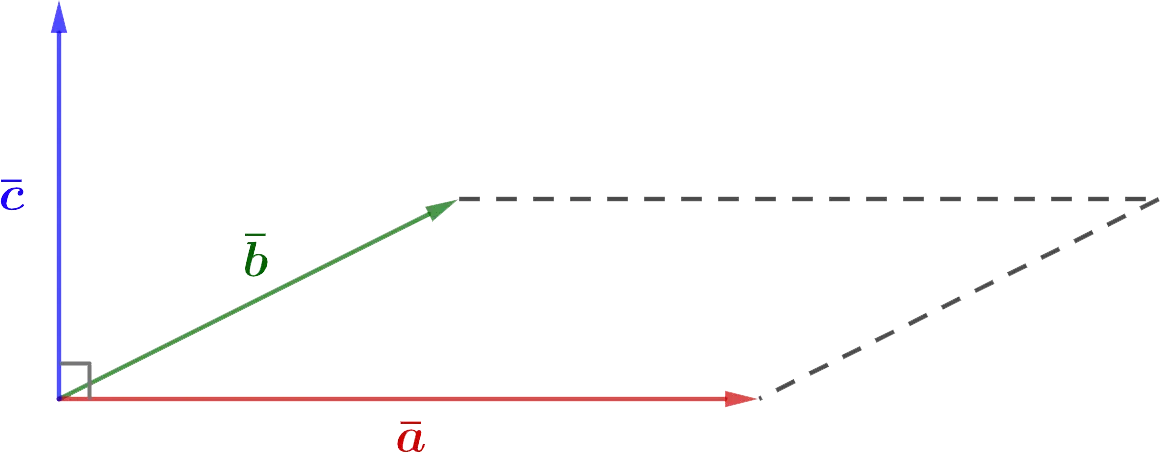
Vector length c is equal to the area of ​​the parallelogram constructed using the vectors a и b.

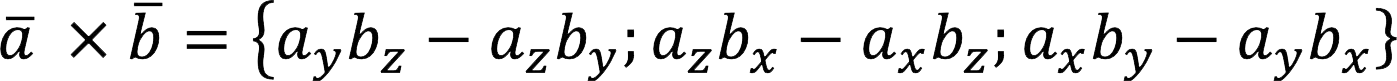
In this case, c perpendicular to the plane in which they are a и b, and is located so that the least rotation from a к b was performed counterclockwise (from the point of view of the end of the vector).

Cross product formula

Product of vectors a = {a_x; to_y,_z} i b = {b_x; b_y, b_z} is calculated using one of the formulas below:

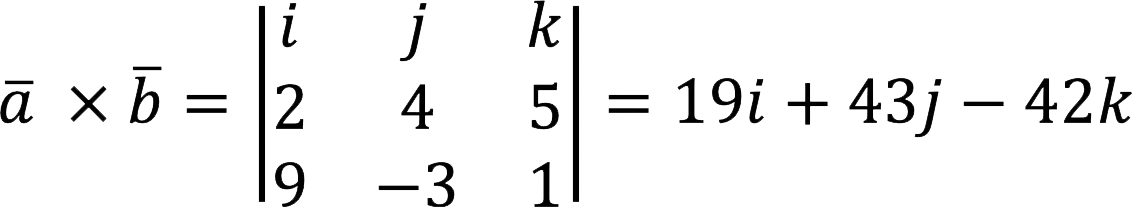
Cross product properties

1. The cross product of two non-zero vectors is equal to zero if and only if these vectors are collinear.

[a, b] = 0, if a || b.

2. The module of the cross product of two vectors is equal to the area of ​​the parallelogram formed by these vectors.

S_parallel = |a x b|

3. The area of ​​a triangle formed by two vectors is equal to half of their vector product.

S_Δ = ¹/₂ · |a x b|

4. A vector that is a cross product of two other vectors is perpendicular to them.

c ⟂ a, c ⟂ b.

5. a x b = –b x a

6. (m a) x a = a x (m b) = m (a x b)

7. (a + b) x c = a x c + b x c

Example of a problem

Compute the cross product a = {2; 4; 5} и b = {9; -two; 3}.

Decision:

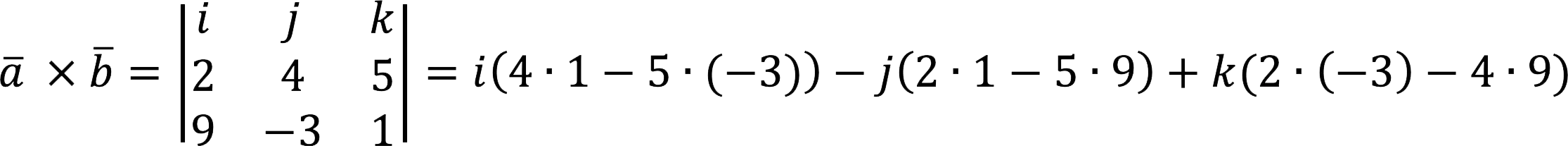
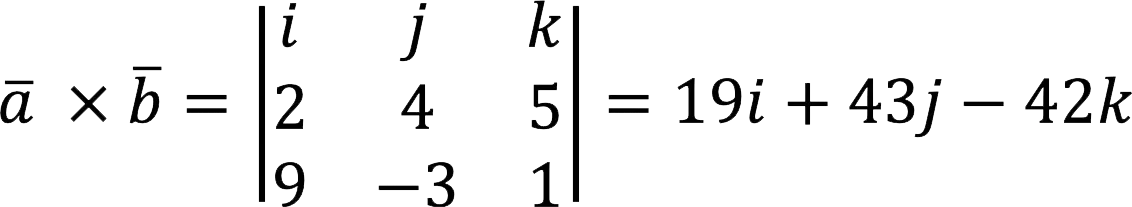
Answer: a x b = {19; 43; -42}.