Cosine theorem for a triangle: formula and tasks

In this publication, we will consider one of the main theorems of Euclidean geometry, the cosine theorem, which determines the ratio of sides in a triangle, and also learn how to apply it in practice to solve problems.

Statement and formula of the theorem

In a flat triangle, the square of a side is equal to the sum of the squares of the other two sides minus twice the product of those sides times the cosine of the angle between them.

a² = b² + c² – 2 ⋅ b ⋅ c ⋅ cos a

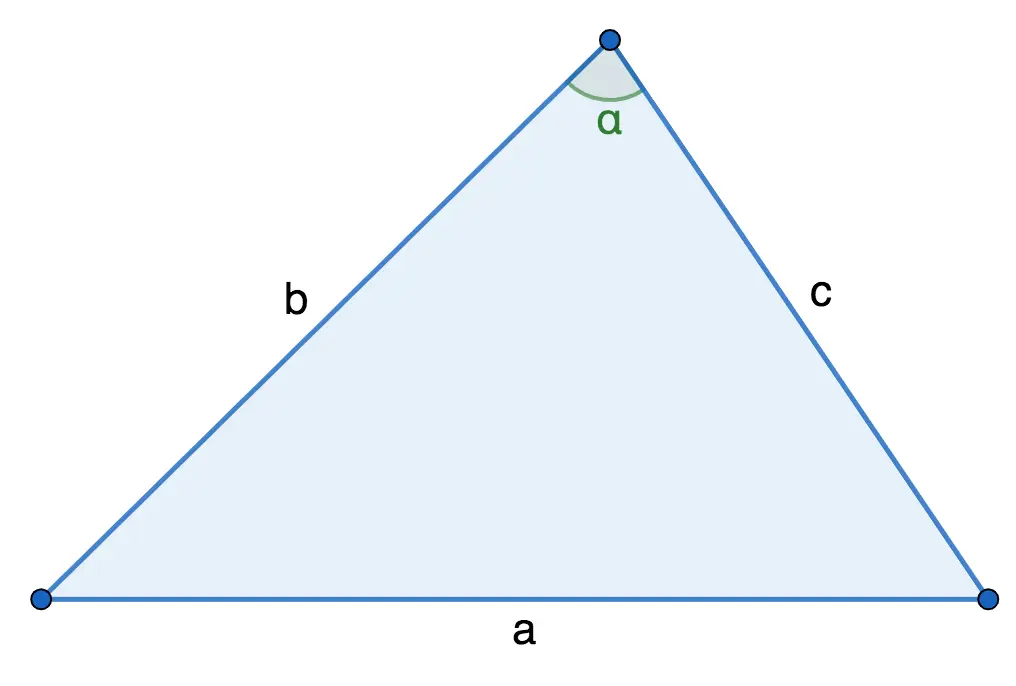
Corollary from the theorem

The formula of the theorem can be applied to find the cosine of an angle in a triangle:

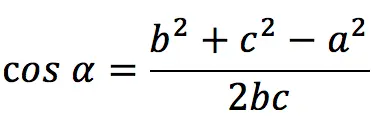
Wherein:

• if b² + c² – and² > 0, then the angle α is acute;
• if b² + c² – and² = 0, then the angle α is equal to 90 degrees (the term of cosines takes the form);
• if b² + c² – and² <0, then the angle α is obtuse.

Examples of tasks

Task 1

In a triangle, the lengths of two sides are known – 5 and 9 cm, as well as the angle between them – 60 °. Find the length of the third side.

Decision:

We apply the formula of the theorem, taking the known sides as b и c, and unknown for a:

a² = 5² + 9² – 2 ⋅ 5 ⋅ 9 ⋅ cos 60° = 25 + 81 – 45 = 61 cm². Therefore, the side a = √61 cm ≈ 7,81 cm.

Task 2

The largest side of the triangle is 26 cm, and the other two are 16 and 18 cm. Find the angle between the smaller sides.

Decision:

Let’s take the bigger side for a. To find the angle between sides b и c, we use the corollary from the theorem:

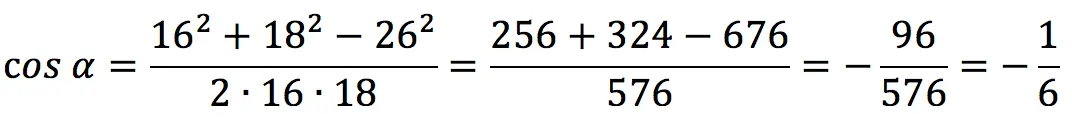
Therefore, the angle α = arccos (-1/6) ≈ 99,59°.