In this publication, we will consider which vectors are called coplanar, and list the conditions for the coplanarity of two, three, or more vectors. We will also analyze examples of solving problems on this topic.
Complanarity conditions for vectors
Vectors lying in the same plane or parallel to it are called coplanar.
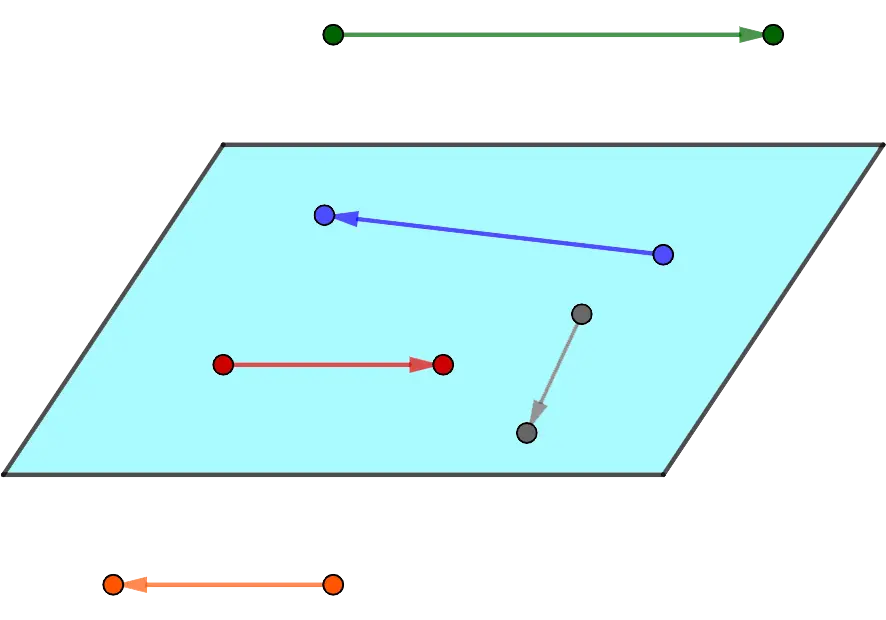
It follows from the definition that any two vectors are coplanar, since one can always find a plane parallel to both of them.
Complanarity conditions:
- For three vectors:
- Their mixed product is zero.
- They are linearly dependent.
- For the nth number of vectors: among them there are at most two linearly independent vectors.
Example of a problem
Let us determine whether the vectors
Solution
To check the complanarity of vectors with given coordinates, we find their mixed product.
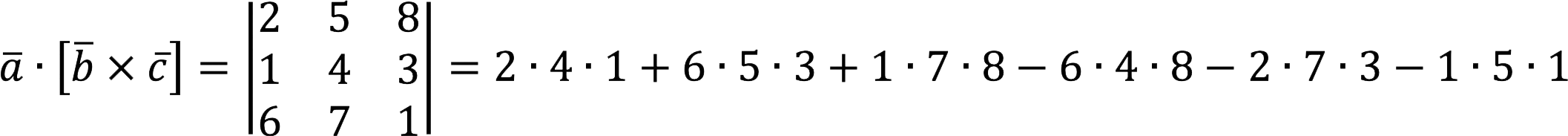
a · [b x c] =
Thus, the vectors are not coplanar, because their mixed product is not equal to zero.









