This publication discusses the trigonometric form of a complex number with an interpretation on the coordinate plane, formulas for calculating the argument and an example for a better understanding of the material presented. It also provides basic information on the exponential form of this type of number.
Trigonometric form of a complex number
Any complex number (excluding zero) of the form
z = |z| ⋅ (cos φ + i ⋅ sin φ)
To make it clearer, we show a complex number on the coordinate plane. In this case, as an example, we will proceed from the fact that a и b Above zero.
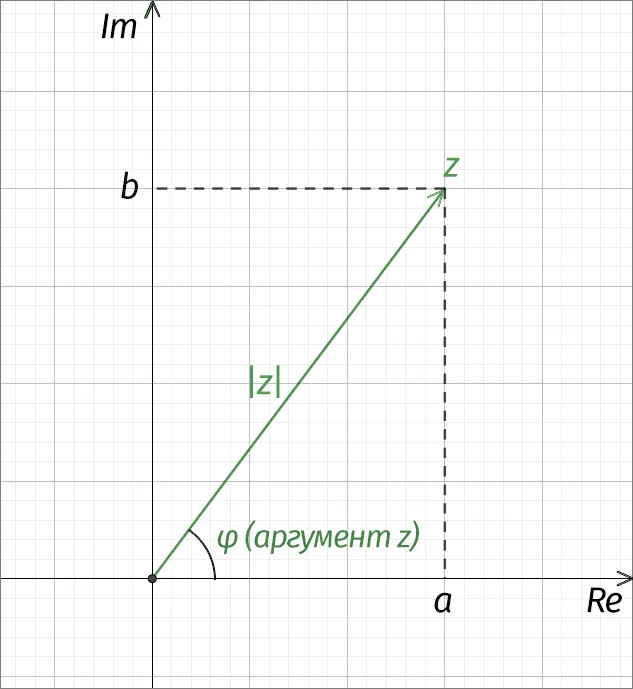
The modulus of a complex number | from | is the distance from the origin to the corresponding point on the complex plane, in other words it is the length of the green vector in the drawing above.
Based on the Pythagorean theorem, the modulus is calculated as follows:
![]()
The argument of a complex number (φ) is the angle between the positive semiaxis of the real axis (RE) and a vector drawn from the origin. Argument does not exist for
The formula for calculating the argument depends on what values uXNUMXbuXNUMXbtake a и b.
» data-order=»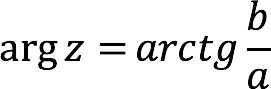 » style=»min-width:63.3684%; width:63.3684%;»>
» style=»min-width:63.3684%; width:63.3684%;»>
» data-order=»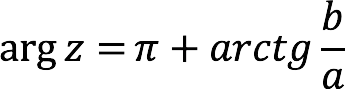 «>
«>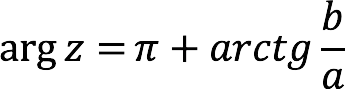
» data-order=»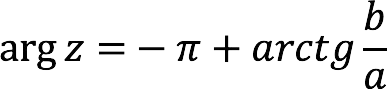 «>
«>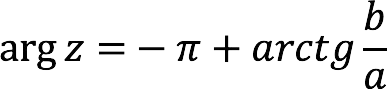
| 1st and 4th coordinate quarters |
| 2nd coordinate quarter |
| 3rd coordinate plane |
Example: represent in trigonometric form the complex number
Decision:
a = 0, b = 3, therefore:
![]()
Since the a = 0, then the vector coincides with the ordinate axis (directed upwards), therefore φ = 90 °.
Thus, the trigonometric form of the number
z = 3 ⋅ (cos 90° + i ⋅ sin 90°)
The exponential form of a complex number
Any complex number (excluding zero) of the form
z = |z| ⋅ e iφ, where:
- | from | – module of a complex number;
- φ is his argument.
Note: The exponential form is used much less frequently than the trigonometric form, so the basic information above should suffice in most cases.









