Basic properties of an ellipse

In this publication, we will consider the main properties of the ellipse, accompanying them with visual drawings for a better perception of the information presented.

Note: we examined the definition of an ellipse, its main elements and the equation in.

Geometric properties of an ellipse

Property 1

Angle between the tangent drawn to the ellipse and the focal radius r₁ equals the angle between the same tangent and the focal radius r₂.

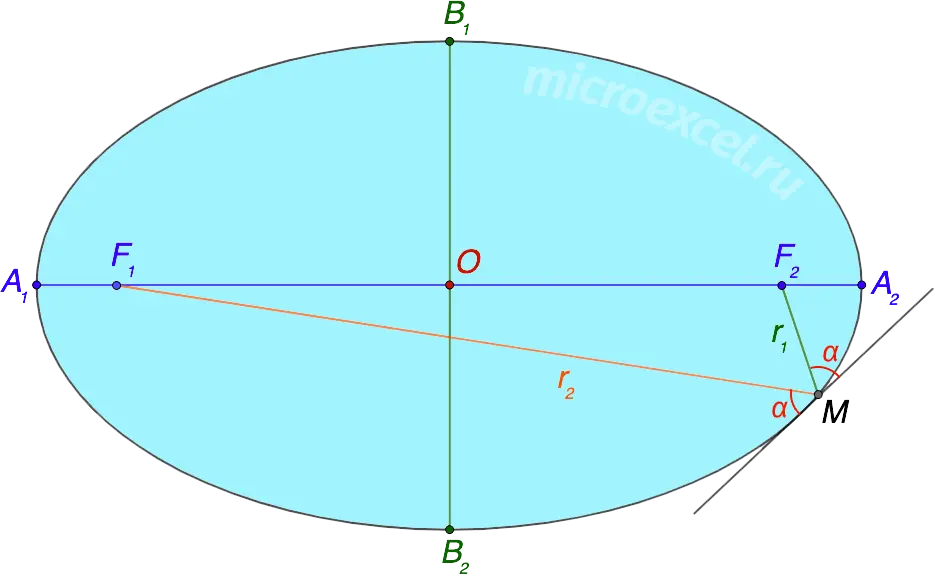
• r₁ и r₂ are the focal radii of the ellipse;
• Point M – the point of contact of the tangent and the ellipse;
• α are equal angles between the tangent and focal radii.

Property 2

The equation of a tangent drawn to an ellipse (touching at a point M) with coordinates (x_My_M) as follows:

Property 3

Suppose an ellipse is crossed by two parallel lines. The segment that connects the midpoints of the segments resulting from the intersection of straight lines and an ellipse will always pass through the center of the figure.

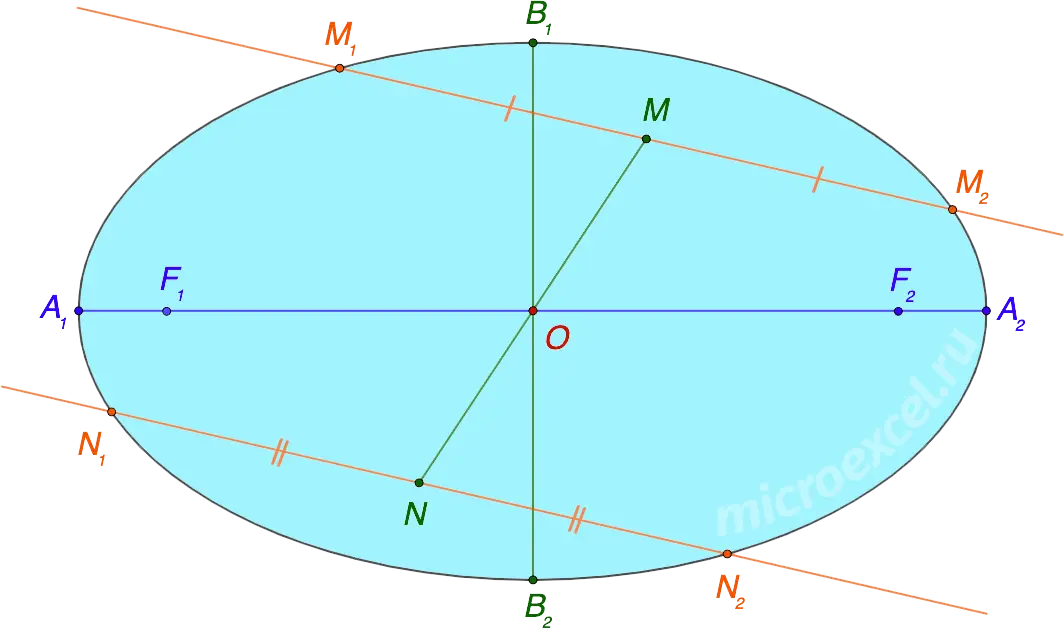
• M₁M₂ и N₁N₂ – segments formed as a result of the intersection of an ellipse by two parallel lines.
• MN – a segment connecting the midpoints M₁M₂ и N₁N₂;
• MN passes through the center of the ellipse O).

Property 4

Let’s say an ellipse with foci F₁ и F₂ inscribed in a triangle ABC.

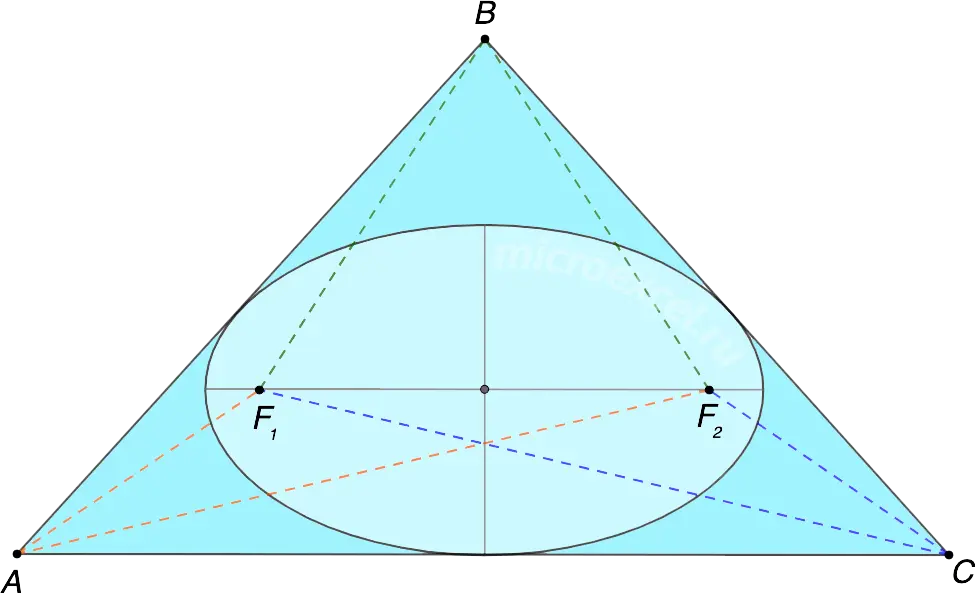
In this case, the relation below is valid:

Optical properties of an ellipse

1. Light from a source located at one of the foci of the ellipse is reflected by it in such a way that the reflected rays intersect at its second focus.
2. Light from a source that is outside the foci of the ellipse is reflected by it in such a way that the reflected rays do not intersect at any focus.