In this publication, we will consider the main properties of the cone, accompanying them with appropriate drawings for a better perception of the information presented.
Note: we examined the definition of a cone, its main elements and varieties in, so we will not dwell on them further.
Cone Properties
The above properties apply to a right circular cone (the most common type of this figure).
Property 1
All generators of a cone have the same length.
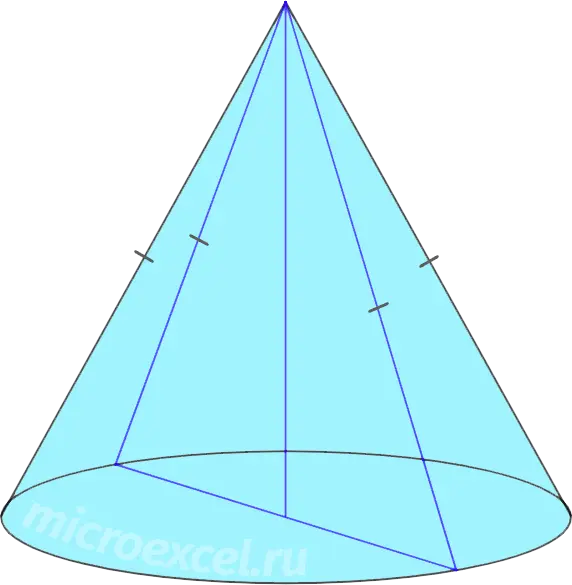
Property 2
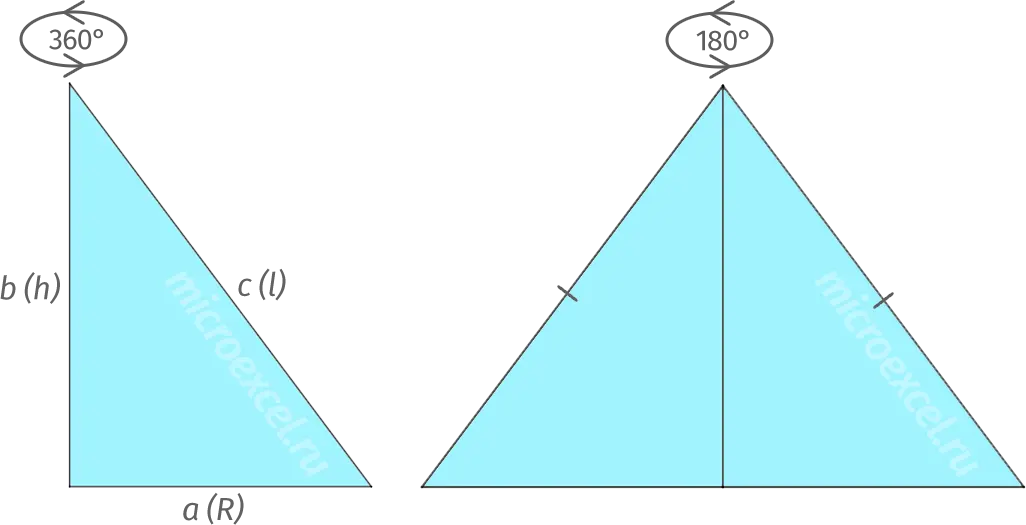
A cone is formed by rotating a right triangle around one of the legs by 360° or an isosceles triangle (consists of two equal right triangles) around its axis by 180°.
Consequences:
- The angles at the base of the cone (i.e. between the base and the generators) are equal.
- The square of the generatrix of a cone (the hypotenuse of a right triangle) is equal to the sum of the squares of its height and the radius of the base (the leg of a right triangle).
c2 = A2 + b2 or l2 = R2 + h2
Property 3
When a cone is intersected by any plane parallel to its base, a circle (conic section) is obtained. The figure formed between the base and the given circle is a truncated cone.

Other conic section options:
1. If the cutting plane is not parallel to the base of the cone, then the result of the section is an ellipse.

2. If the cutting plane passes through the base of the cone, then the result of the section is a parabola/hyperbola.
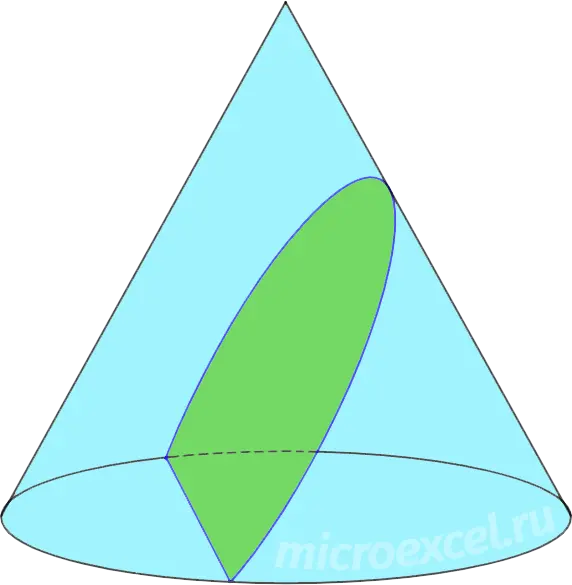
3. The result of a section of a cone by a plane passing through its axis (or height) is an isosceles triangle.

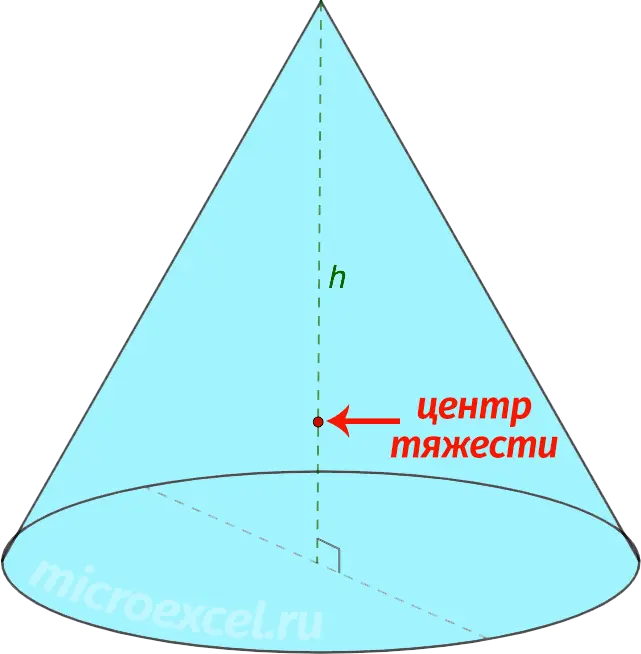
Property 4
The center of gravity of the cone is located at a quarter of its height, counting from the base.