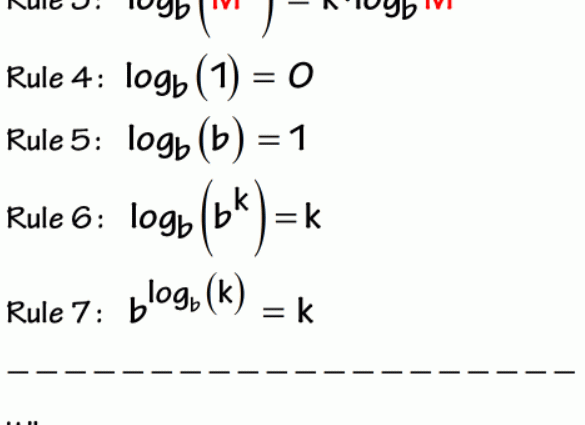Logarithm of a number b by reason a is the inverse function of the exponential equation b = a x.
Written as log a b = x and means the following: to what extent x we need to raise the number a, To obtain b.
Wherein:
- base a must be a positive number, not equal to one (a>0, a≠1);
- number b must be positive (b>0), because for a negative value of the root of the equation (x) does not exist (if positive, the root is one).
Formula of the basic logarithmic identity
If the above conditions are met, then the following expression is true, which has a special name – basic logarithmic identity:
a log a b = b
Consequence:
If log a b = log a cthen a log a b = a log a c. And that means b = c.
examples:
- 6 log 6 4 = 4
- 7 log 7 9 = 9
- 12 log 12 5 = 5