Angle between line and plane

In this publication, we will consider what the angle between a straight line and a plane is, and by what formula it is calculated. We will also analyze an example of solving a problem on this topic.

Finding an angle

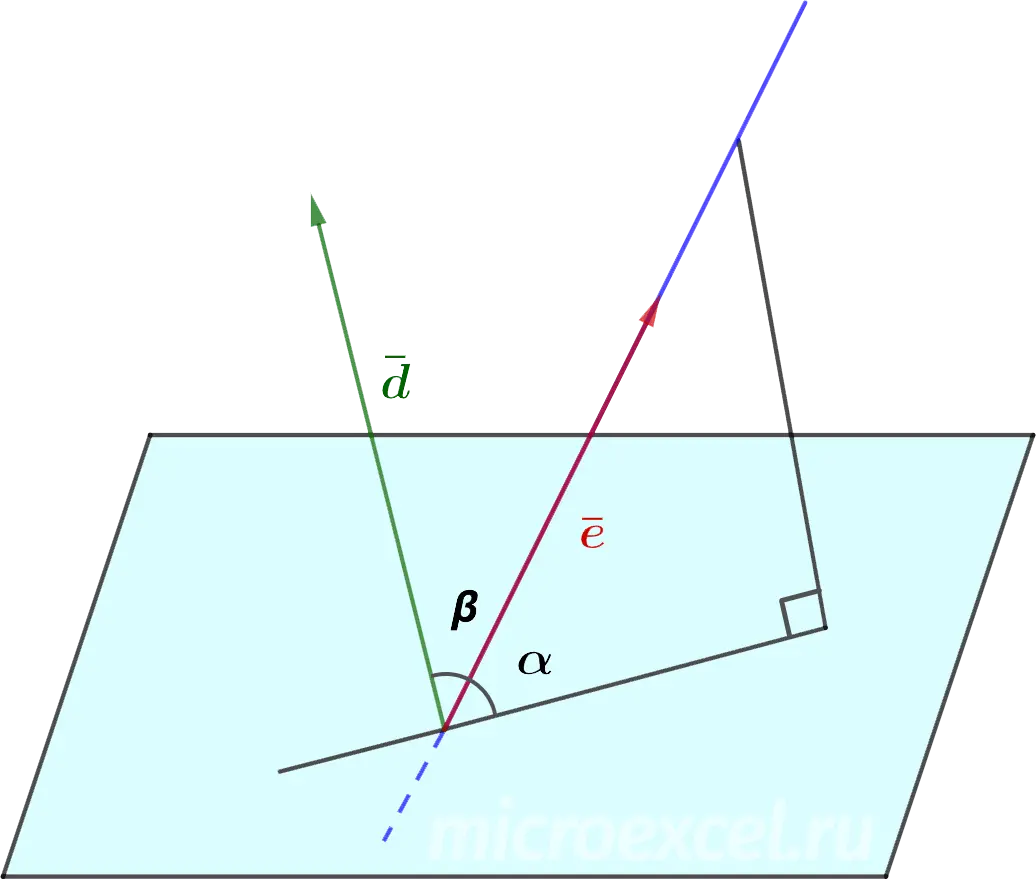
The angle between a straight line and its projection onto a plane is angle between line and plane.

Calculation formula

Suppose there is a plane given by the equation Ax + By + Cz + D = 0, as well as the direction vector of the straight line e = {l; m; n}.

The sine of the angle between a straight line and a plane is calculated by the formula:

The plane normal is defined as follows:

d = {A; B; C}

The cosine of the angle between the normal to the plane and the directing vector of the line can be found as follows:

Note: without α = cos β

Example of a problem

Given a plane 2x + y – 3z + 5 = 0, as well as the direction vector of the straight line e = {3; -two; 2}. Find the angle between the line and the plane.

Decision:

Let’s use the formula above, substituting the values ​​we know into it:

Therefore, the angle is approximately 23,4° (arcsin 0,397).