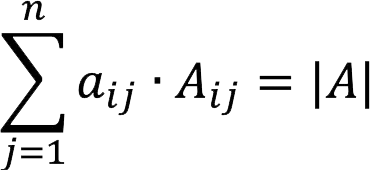Algebraic Matrix Complement

In this publication, we will consider the definition and properties of the algebraic complement of a matrix, give a formula with which it can be found, and also analyze an example for a better understanding of the theoretical material.

Definition and finding of algebraic complement

Algebraic addition A_ij to element a_ij the determiner nth order is the number A_ij = (-1)^{i + j} M_ijWhere M – this is .

Example

Calculate the algebraic complement A₃₂ к a₃₂ definer below:

Solution

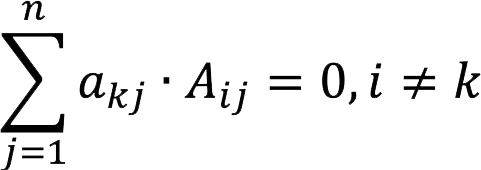
Algebraic Complement Properties

1. If we sum the products of the elements of an arbitrary string and the algebraic additions to the elements of the string i determinant, we get a determinant in which instead of the string i there is a given arbitrary string.

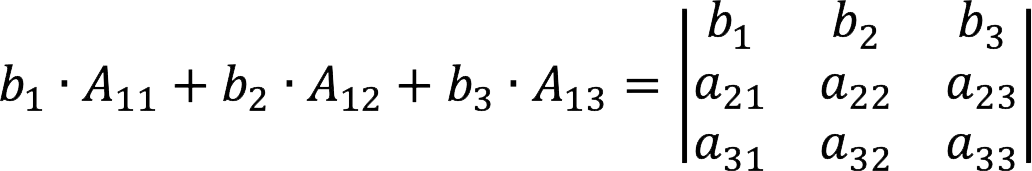
2. If we sum up the products of the elements of the row (column) of the determinant and the algebraic additions to the elements of another row (column), then we get zero.

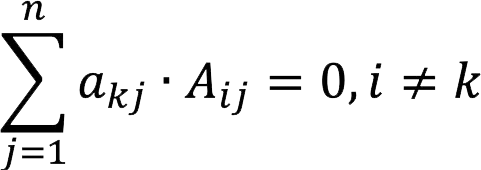
3. The sum of the products of the elements of the row (column) of the determinant and the algebraic additions to the elements of the given row (column) is equal to the determinant of the matrix.